- 通过拟合整个奖励分布进行强化学习

1. Motivation
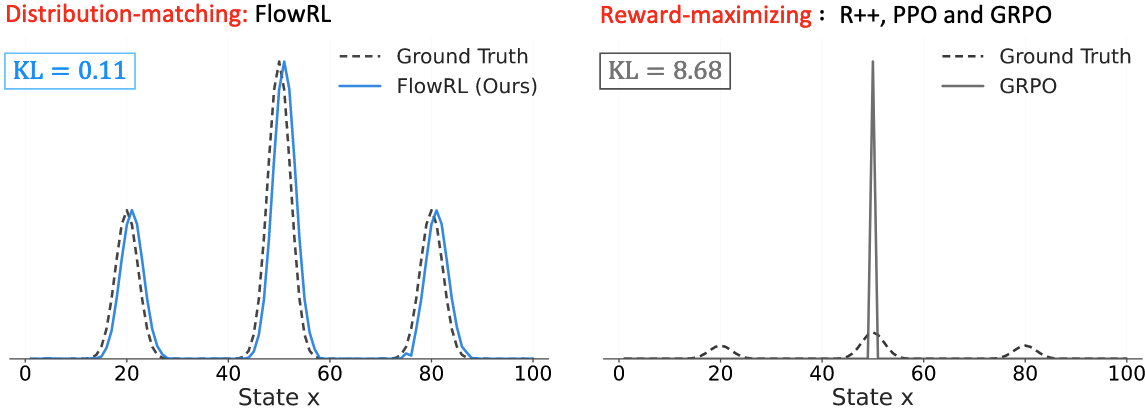
目前的主流RL方法(如REINFORCE++、PPO、GRPO等)都以最大化奖励为目标,这种范式会倾向于将模型过拟合到奖励分布中的高概率区域,导致生成的推理路径的多样性受限,还削弱了模型对那些出现频率较低但正确的推理路径的泛化能力。特别是在需要长CoT的复杂推理任务中,这种缺陷会更加显著。
近期的研究引入了一些方法来缓解这种过拟合问题,比如说:
- DAPO:调整clip ratio
- Entropy Adv:在优势中加入熵正则化
- Qwen-82法则:仅优化20%的高熵token
这些方法通过动态调整训练数据的分布,在训练过程中隐式地增强推理路径的多样性。
这引出了一个根本性的问题:我们应该如何增加探索的多样性,以防止RL训练过程过早地收敛到单一的解空间中?
文章提出了FlowRL,一种将策略与整个奖励分布进行对齐的策略优化算法,旨在鼓励策略学习到奖励分布中的多种模式。FlowRL将优化目标从“奖励最大化”转变为“奖励分布匹配”,从而实现了更高效的探索,克服了以往RL方法中可能存在的模式坍缩问题。
FlowRL的核心思想是引入一个可学习的归一化函数 (partition function),将数值奖励归一化为一个目标分布,并通过最小化策略和目标分布之间的逆KL散度来实现策略的匹配。
2. Methodology
2.1. 从最大化奖励到匹配奖励分布
为了防止模型过拟合到奖励分布中的高概率区域导致模式崩溃,FlowRL提出将策略与整个奖励分布进行对齐,而不是仅仅最大化奖励。然而在长CoT推理任务中,我们无法拿到整个奖励分布,只能拿到每个样本的奖励,我们也无法通过采样所有可能的轨迹来估计奖励分布。
为了解决这个问题,FlowRL引入了一个可学习的归一化函数 (partition function) $Z_{\phi}(x)$,将数值奖励归一化为一个目标分布。这样一来,我们就可以最小化策略和目标奖励分布之间的逆KL散度:
\[\begin{equation} \min _{\theta} \mathcal{D}_{\mathrm{KL}}\left(\pi_{\theta}(y \mid x) \left\| \frac{\exp (\beta r(x, y))}{Z_{\phi}(x)} \right.\right) \label{eq:flowrl-kl} \end{equation}\]因此,我们的目标策略就是:
\[\begin{equation} \pi_{\theta}(y \mid x) \propto \exp (\beta r(x, y)) \end{equation}\]Note:之所以选择逆KL散度,是因为我们只能从策略 $\pi_{\theta}(y \mid x)$ 中采样,而无法直接从目标奖励分布中采样。
这个训练目标会鼓励策略根据奖励值 $r(x, y)$ 来生成多样且高奖励的推理路径。
为了让公式 \eqref{eq:flowrl-kl} 更加贴近强化学习的优化目标,作者利用GFlowNet中的结论,将原问题转换为下面的形式:
\[\begin{equation} \min _{\theta} \mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\left( \log Z_{\phi}(x) + \log\pi_{\theta}(y \mid x) - \beta r(x, y) \right)^2\right] \label{eq:flowrl-obj} \end{equation}\]公式 \eqref{eq:flowrl-kl} 和 \eqref{eq:flowrl-obj} 的等价性证明放在附录1中。
2.2. FlowRL
尽管我们已经有了匹配奖励分布的目标函数,但在长CoT任务中,仍然会存在下面两大挑战:
挑战1:长CoT导致的梯度爆炸。公式 \eqref{eq:flowrl-obj} 被称为轨迹平衡损失 (trajectory balance loss)。这是一种序列级别的目标函数,将它用于长CoT任务是,可能会导致梯度爆炸和更新不稳定问题。具体而言,对数概率 $\log \pi_{\theta}(y \mid x)$ 可以被分解为 $\sum_{t}\log\pi_{\theta}(y_t \mid y_{\lt t},x)$,这可能导致梯度的范数随着序列长度线性增长,引发数值不稳定。
挑战2:实际训练中会存在off-policy因素。基于KL散度的轨迹平衡损失需要使用完全on-policy的策略进行采样,即从 $\pi_{\theta}$ 中采样来更新 $\theta$。然而,主流的RL算法往往使用micro-batchl来更新参数,即使用 $\pi_{\theta_{old}}$ 来采样,复用到多步更新中,从而提高数据效率。这种采样机制上的不匹配会导致策略和目标分布之间的不一致,从而影响优化效果。
为了解决这些问题,作者首先修改了一下公式 \eqref{eq:flowrl-obj} 中的目标函数。
- 首先,作者在目标分布 $\exp(\beta r(x, y))$ 中增加了reference model项,作为对奖励分布的一个先验约束,即:$\exp(\beta r(x, y))\cdot\pi_{\text{ref}}(y \mid x)$。
- 其次,作者将奖励值 $r(x,y)$ 变为GRPO中的组相对优势,即 $\hat{r}(x,y) = (r(x,y) - \text{mean}(r))/\text{std}(r)$。
因此,我们得到了下面的目标函数:
\[\begin{equation} \min _{\theta} \mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\left( \log Z_{\phi}(x) + \log\pi_{\theta}(y \mid x) - \beta \hat{r}(x, y)-\log\pi_{\text{ref}}(y \mid x) \right)^2\right] \end{equation}\]为了防止长CoT导致的梯度爆炸,作者通过长度归一化对奖励进行了缩放 (reward shaping),即变为 $\frac{1}{\lvert y\rvert}\log\pi_{\theta}(y \mid x)$。
同时,为了消除off-policy因素,作者参考PPO中的clipped surrogate objective,引入了一个重要性采样系数 $w = \text{clip}\left(\frac{\pi_{\theta}(y \mid x)}{\pi_{\theta_{old}}(y \mid x)}, 1-\epsilon, 1+\epsilon\right)$。
因此,最终FLowRL的目标函数为:
\[\begin{equation} \mathcal{L}_{\text{FlowRL}} = w\cdot\left( \log Z_{\phi}(x) + \frac{1}{\lvert y\rvert}\log\frac{\pi_{\theta}(y \mid x)}{\pi_{\text{ref}}(y \mid x)} - \beta \hat{r}_{i}(x, y) \right)^2 \label{eq:flowrl-final} \end{equation}\]我们可以证明(附录2),公式 \eqref{eq:flowrl-final} 是在同时最大化奖励值和策略的熵:
\[\begin{equation} \max_{\theta}\mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[ \underbrace{\beta r(x,y)}_{\text{reward}} -\underbrace{\log Z_{\phi}(x)}_{\text{normalization}} +\underbrace{\log \pi_{\text{ref}}(y \mid x)}_{\text{prior alignment}} \right] +\underbrace{\mathcal{H}(\pi_{\theta})}_{\text{entropy}} \label{eq:flowrl-entropy} \end{equation}\]这种范式会鼓励策略去探索更多高质量解,从而在推理任务上实现更加多样化且更具泛化能力的行为。
3. Experiments
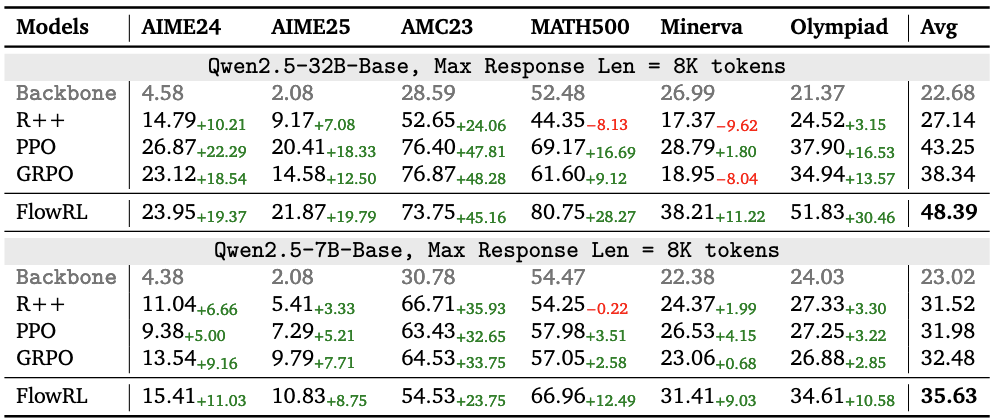
3.1. 数学推理能力
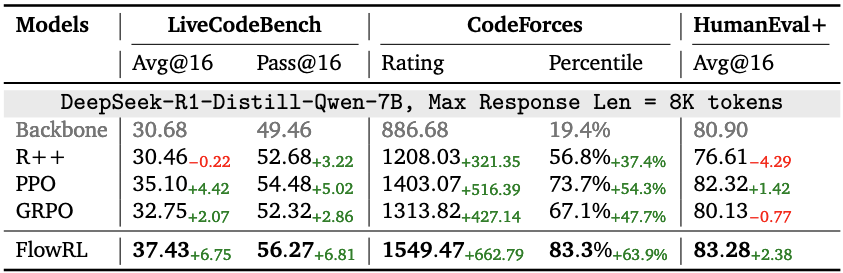
3.2. 代码能力
3.3. Case Study
可以看到FlowRL确实能够避免策略的过拟合问题,减少了复读机现象。

Appendix
Apd.1. 公式 \eqref{eq:flowrl-kl} 和 \eqref{eq:flowrl-obj} 的等价性
首先我们分析公式 \eqref{eq:flowrl-kl} 的梯度形式:
\[\begin{equation} \begin{aligned} &\nabla_{\theta} \mathcal{D}_{\mathrm{KL}}\left(\pi_{\theta}(y \mid x) \left\| \frac{\exp (\beta r(x, y))}{Z_{\phi}(x)} \right.\right)\\ &=\nabla_{\theta}\int\pi_{\theta}(y \mid x)\log\left[\frac{\pi_{\theta}(y\mid x)\cdot Z_{\phi}(x)}{\exp (\beta r(x, y))}\right] \mathrm{d}y\\ &=\int\nabla_{\theta}\pi_{\theta}(y \mid x)\log\left[\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))}\right] \mathrm{d}y+\int\pi_{\theta}(y \mid x)\nabla_{\theta}\log\left[\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))}\right] \mathrm{d}y\\ &=\int\pi_{\theta}(y \mid x)\nabla_{\theta}\log\pi_{\theta}(y \mid x)\log\left[\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))}\right] \mathrm{d}y+\underbrace{\int \pi_{\theta}(y \mid x)\nabla_{\theta}\log\pi_{\theta}(y \mid x)\mathrm{d}y}_{=\nabla_{\theta}\int \pi_{\theta}(y \mid x)\mathrm{d}y=0}\\ &=\mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\log\left(\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))}\right)\cdot\nabla_{\theta}\log\pi_{\theta}(y \mid x)\right]\\ \end{aligned} \end{equation}\]同样,我们可以证明公式 \eqref{eq:flowrl-obj} 的梯度形式为:
\[\begin{equation} \begin{aligned} &\nabla_{\theta} \mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\left( \log Z_{\phi}(x) + \log\pi_{\theta}(y \mid x) - \beta r(x, y) \right)^2\right]\\ &=\mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\nabla_{\theta} \left(\log\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))}\right)^2\right] \\ &=2\cdot \mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\log\left(\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))}\right)\cdot\nabla_{\theta}\log\pi_{\theta}(y \mid x)\right]\\ &\propto \nabla_{\theta} \mathcal{D}_{\mathrm{KL}}\left(\pi_{\theta}(y \mid x) \left\| \frac{\exp (\beta r(x, y))}{Z_{\phi}(x)} \right.\right) \end{aligned} \end{equation}\]因此,公式 \eqref{eq:flowrl-kl} 和 \eqref{eq:flowrl-obj} 在梯度上只相差了一个系数,二者是等价的。
Apd.2. 公式 \eqref{eq:flowrl-final} 和 \eqref{eq:flowrl-entropy} 的等价性
\[\begin{equation} \begin{aligned} &\arg\min_{\theta}\mathcal{D}_{\mathrm{KL}}\left(\pi_{\theta}(y \mid x) \left\| \frac{\exp (\beta r(x, y))\cdot\pi_{\text{ref}}(y \mid x)}{Z_{\phi}(x)} \right.\right)\\ &=\arg\min_{\theta}\int\pi_{\theta}(y \mid x)\log\left[\frac{Z_{\phi}(x)\pi_{\theta}(y\mid x)}{\exp (\beta r(x, y))\pi_{\text{ref}}(y \mid x)}\right] \mathrm{d}y\\ &=\arg\max_{\theta}\left\{ \mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[\log\left(\frac{\exp (\beta r(x, y))\pi_{\text{ref}}(y \mid x)}{Z_{\phi}(x)}\right)\right] -\int\pi_{\theta}(y \mid x)\log\pi_{\theta}(y \mid x) \mathrm{d}y \right\}\\ &=\arg\max_{\theta}\left\{ \mathbb{E}_{y\sim\pi_{\theta}(\cdot \mid x)}\left[ \beta r(x,y)-\log Z_{\phi}(x)+\log \pi_{\text{ref}}(y \mid x) \right]+\mathcal{H}(\pi_{\theta}) \right\} \end{aligned} \end{equation}\]得证。