RFT的熵动力学分析

EntDymanic_cover

1. Introduction

在本系列的前两篇文章中，我们已经分别介绍了策略熵、策略梯度算法对熵的影响，并且列举了一系列防止熵坍塌（即熵安全）的方法。在这篇论文中，作者以一个更微观的角度来看待策略熵的变化，并且将各种各样的熵安全方法在统一的理论框架下进行了总结和分类。

RFT面临着探索和利用 (Exploration-Exploitation) 的权衡难题，我们在RFT的过程中经常会遇到策略熵坍塌 (Entropy Collapse) 现象：随着训练进行，策略的输出分布迅速尖锐化，模型倾向于生成重复的、高置信度的“安全”回复，导致多样性丧失，最终陷入局部最优。

本文回答了以下三个问题：

为什么奖励高分答案会导致策略熵的下降？
每个token的更新如何影响策略熵？
如何从理论层面设计更加合理的熵安全策略？

2. RFT中的熵动力学分析

为了更好地分析RFT过程中的熵动力学，作者首先量化了单个token的更新会对策略熵产生什么影响。基于此，作者推导得到了GRPO算法对于策略熵的改变。

2.1. 单个token的影响

我们首先定义RFT更新的原子操作：我们对第 $k$ 个token $a_k$ 的logits $z_k$ 进行一个微小的扰动：

\[\begin{equation} \Delta z=\varepsilon\cdot e_k \end{equation}\]

其中，$e_k$ 是单位基向量，即第 $k$ 个元素为1，其他为0。$\varepsilon$ 是梯度回传计算的更新向量。注意，$\varepsilon$ 的符号代表了更新的方向：

$\text{sign}(\varepsilon)=1$ 表示奖励token $a_k$，增加 $z_k$。
$\text{sign}(\varepsilon)=-1$ 表示惩罚token $a_k$，减少 $z_k$。

下面的引理描述了这个扰动如何传递影响到整个策略分布：

Lemma 1 (first-order change of policy distribution). 对 $a_k$ 施加上述的扰动 $\Delta z$ 后，策略分布 $\pi$ 的变化量为：

\[\begin{equation} \Delta\pi_i= \begin{cases} \varepsilon\pi_k(1-\pi_k), & i=k\\ -\varepsilon\pi_k\pi_i, & i\neq k \end{cases} \label{eq:lemma-1} \end{equation}\]

Lemma 1 非常直观地说明了Softmax策略的性质：增加某个token的概率需要减少其他所有token的概率。此外，其他所有token概率减少的比例是相同的，只决定于 $k$，因为：

\[\begin{equation} \frac{\Delta \pi_i}{\pi_i} = \begin{cases} \varepsilon(1-\pi_k), & i=k\\ -\varepsilon\pi_k, & i\neq k \end{cases} \end{equation}\]

这表明，当一个token的logits增加时，其他所有token的概率都会等比例的减少。反之亦然。

基于此，我们就能够量化策略上的一阶改变量。

对于词表中的任意token $a_i$，我们定义其熵判别器 (Entropy Discriminator) 为：

\[\begin{equation} S_i:= \pi_i(\mathcal{H}(\pi) + \log\pi_i) \end{equation}\]

其中，$\mathcal{H}(\pi)$ 是策略分布 $\pi$ 的香农熵：

\[\begin{equation} \mathcal{H}(\pi) =-\sum_{i=1}^{V}\pi_i\log\pi_i \end{equation}\]

对于被更新的token $a_k$，我们特别记其熵判别器为 $S_{\ast}=S_k$。

下面的定理1描述了 $a_k$ 的更新导致的策略熵的变化：

Theorem 1 (first-order change of policy entropy). 对 $a_k$ 更新 $\Delta z=\varepsilon\cdot e_k$ 后，策略熵的变化量为：

\[\begin{equation} \Delta\mathcal{H} =-\varepsilon S_{\ast}+O(\varepsilon^2) \label{eq:theorem-1} \end{equation}\]

定理1表明：策略熵是增加还是减少，取决于更新方向 $\varepsilon$ 和判别器 $S_{\ast}$ 的符号。其中，判别器 $S_{\ast}$ 的符号又取决于 $\mathcal{H}(\pi) + \log\pi_k$：

当 $\log\pi_k\lt \mathcal{H}(\pi)$ 时，$S_{\ast}\lt 0$，此时token $a_k$ 是相对低概率的
当 $\log\pi_k\gt \mathcal{H}(\pi)$ 时，$S_{\ast}\gt 0$，此时token $a_k$ 是相对高概率的

因此，我们可以得到如下结论：

奖励高概率token：此时 $\varepsilon\gt 0,S_{\ast}\gt 0$，即 $\Delta\mathcal{H}\lt 0$。这是导致RFT中熵坍塌的主要原因：模型倾向于利用已知的高概率路径，奖励这些路径会进一步降低熵。
奖励低概率token：此时 $\varepsilon\gt 0,S_{\ast}\lt 0$，即 $\Delta\mathcal{H}\gt 0$。这时策略被鼓励大胆探索，因此会熵增。
惩罚高概率token：此时 $\varepsilon\lt 0,S_{\ast}\gt 0$，即 $\Delta\mathcal{H}\gt 0$。这迫使策略放弃当前的高概率路径，寻找新解。

2.2. 推广到GRPO更新

在使用GRPO训练时，我们的目标函数为：

\[\begin{equation} \mathcal{J}_{\text{GRPO}}(\theta) = \frac{1}{\sum_{i=1}^G\vert o_i\vert}\sum_{i=1}^G\sum_{j=1}^{\vert o_i\vert} \min\left( r_{i,t}(\theta)A_i, \text{clip}(r_{i,t}(\theta),1-\varepsilon_l,1+\varepsilon_h)A_i \right) \end{equation}\]

其中，

\[\begin{equation} \begin{aligned} A_i &=\frac{r_i-\text{mean}\left(\lbrace r_j \rbrace_{j=1}^G\right)}{\text{std}\left(\lbrace r_j \rbrace_{j=1}^G\right)}\\ r_{i,t}(\theta) &=\frac{\pi_{\theta}(a_{i,t}\mid a_{i,\lt t})}{\pi_{\theta_{\text{old}}}(a_{i,t}\mid a_{i,\lt t})} \end{aligned} \end{equation}\]

因此，对于单个token $a_k$，它对整个训练目标的贡献可以写为：$\pi_k/\pi_k’\cdot A$，其中，$\pi_k’=\pi_{\theta_{\text{old}}}(a_k)$，$A$ 是优势项。我们可以用下面的代理损失来描述：

\[\begin{equation} \mathcal{L}=r\cdot A\cdot\log\pi_k \end{equation}\]

因此，当学习率为 $\eta$ 时，logits的更新量为：

\[\begin{equation} \begin{aligned} \Delta z &=\eta\nabla_z\mathcal{L}\\ &=\eta r A\nabla_z\log\pi_k\\ &=\alpha\nabla_z\log\pi_k\\ &=\alpha\frac{1}{\pi_k}\nabla_z\pi_k\\ &=\alpha\frac{1}{\pi_k}\pi_k(e_k-\pi)\\ &=\alpha(e_k-\pi) \end{aligned} \end{equation}\]

其中，$\alpha=\eta r A$ 称为有效步长。

下面的定理2说明了在GRPO的场景下，单个token $a_k$ 的更新所导致的策略熵变化量。

Theorem 2 (change of policy entropy by GRPO). GRPO算法对策略熵的变化量为：

\[\begin{equation} \Delta\mathcal{H} =-\alpha\left( S_{\ast}-\mathbb{E}_{i\sim \pi}\left[ S_i\right] \right)+O(\alpha^2) \label{eq:theorem-2} \end{equation}\]

值得指出的是，误差项 $O(\alpha^2)$ 在实际场景下是非常小的。这是因为 $\alpha=\eta r A$，其中学习率 $\eta$ 一般是 $10^{-6}$ 量级，重要性采样系数会被clip到1附近，优势项 $A$ 会经过组归一化，一般也不会太大。因此，$\alpha\ll 1$ 基本都能满足。

定理2表明，在完整的一次梯度更新下，策略熵的变化不仅仅只取决于 $S_{\ast}$，而是取决于 $S_{\ast}$ 相对于均值 $\mathbb{E}[S_i]$ 的偏差。我们可以从这个结果中看到一些【动态baseline】的思想，即系统会根据当前的策略分布来衡量某个token更新对整体策略熵的影响，而不是一个固定值。

基于定理2，作者进一步证明了如下两个推论：

Corollary 1 (entropy change of a token with online GRPO optimization). 当我们使用 on-policy 采样时，策略熵改变量的改变量期望为0：

\[\begin{equation} \begin{aligned} \mathbb{E}_{k\sim\pi}\left[S_k-\mathbb{E}_{i\sim \pi}\left[ S_i\right]\right] &=\mathbb{E}_{k\sim\pi}\left[ \pi_k(\mathcal{H}(\pi)+\log\pi_k) -\sum_{i=1}^V\pi_i^2(\mathcal{H}(\pi)+\log\pi_i) \right]\\ &=\sum_{k=1}^V\pi_k^2(\mathcal{H}(\pi)+\log\pi_k)-\sum_{k=1}^V\pi_i^2(\mathcal{H}(\pi)+\log\pi_i)\\ &=0 \end{aligned} \end{equation}\]

Corollary2 (entropy change of a batch with online GRPO optimization). 当我们使用 on-policy 采样时，策略熵改变量的改变量期望为0：

\[\begin{equation} \mathbb{E}_{t\in\mathcal{T}_{B}}\left[S_{\ast}^t-\mathbb{E}_{i\sim \pi}\left[ S_i^t\right]\right]=0 \end{equation}\]

这两个推论告诉我们，熵判别器的偏移量 $S_{\ast}-\mathbb{E}[S_i]$ 在online sampling下表现出比较好的分散性质。因此，调节熵动力学的一种简单而有效的方法就是根据这个偏移量来对token进行约束。

3. Entropy Discriminator Guided Clipping

上面的理论分析为我们提供了一个全新的看待策略熵的视角：RFT的熵动力学和熵判别器 $S_{\ast}$ 之间存在着紧密的联系。

基于这种细粒度的分析，我们可以精确地找出那些容易导致熵坍塌的token，并对其加以约束，从而对训练过程中的熵进行精细而灵活的控制。

3.1. Clip-B: Batch-Normalized Entropy-Discriminator Clipping

给定一个batch $B$，其中所有的token为 $\mathcal{T}_{B}$。Clip-B的流程如下：

对于 $\mathcal{T}{B}$ 中的所有token，计算其熵判别器分数：$S{\ast}=\pi_k(\mathcal{H}(\pi)+\log\pi_k)$。
计算batch内判别器分数的均值 $\overline{S}=\mathbb{E}{i\in\mathcal{T}{B}}\left[S_i\right]$ 和标准差 $\sigma$。
生成梯度掩码： $\begin{equation} m_t=\mathbb{I}(S_\ast-\overline{S}\in[-\mu^-\sigma,\mu^+\sigma]) \end{equation}$ 其中，$\mu^-\sigma$ 和 $\mu^+\sigma$ 分别是判别器分数的下限和上限。
根据掩码 $m_t$ 对其梯度进行裁剪，仅保留 $m_t=1$ 的token的梯度。

Clip-B的优势有以下几点：

计算量非常小，仅需要在一个batch内进行均值和标准差计算。
不需要干预前向过程。
我们可以通过调整 $\mu^+$ 来专门针对那些 $S_{\ast}$ 较高的token，这些token比较容易导致熵坍塌。

3.2. Clip-V: Vocabulary-Level Entropy-Discriminator Clipping

Clip-V是一种理论上更严谨的方法，它在整个词表熵计算判别器分数的均值：$\overline{S}=\mathbb{E}_{i\sim\pi}\left[S_i\right]$

这种方式更加贴合定理2的条件，且能够更加精准地定位离群点，即相对于当前策略来说异常的token。

4. Experiments

4.1. 对比实验

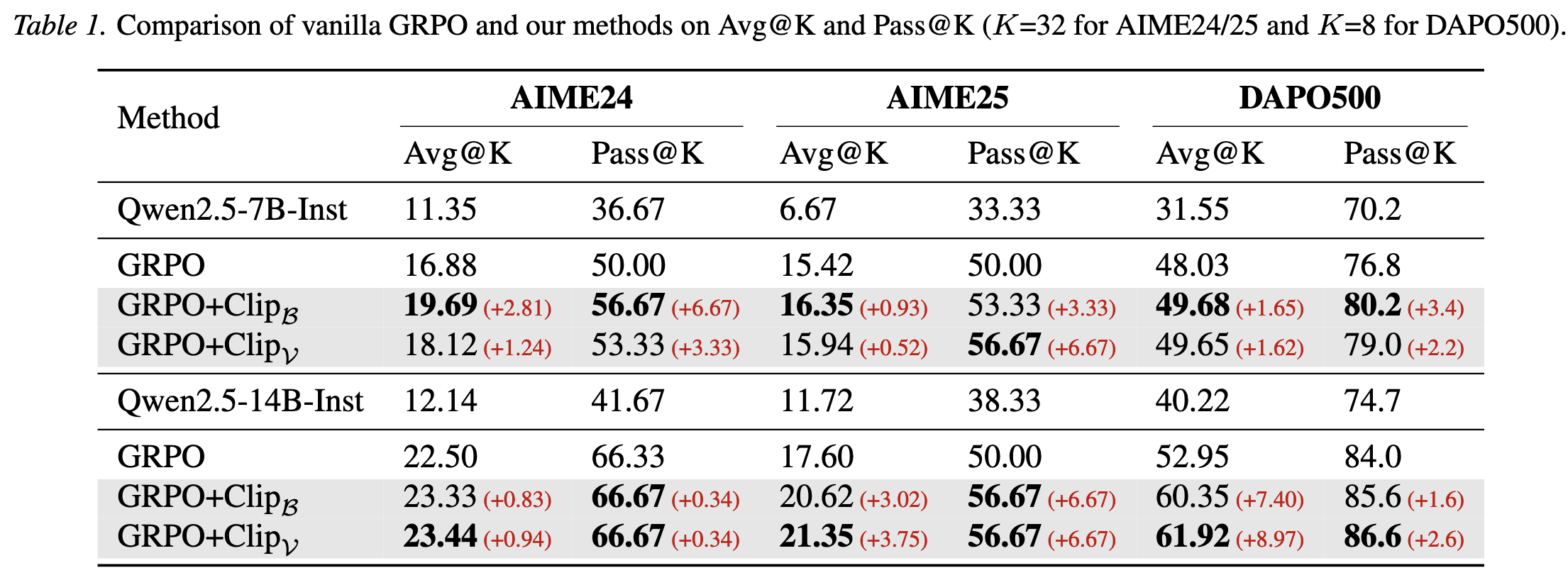
EntDynamic_result

Pass@k显著提升，证明模型探索到了更多样化的解题路径。同时Avg@k也有提升，说明没有牺牲准确率来换取多样性，反而因为多样性的提升导致模型整体能力更强。

4.2. 熵判别器分数的预测能力

作者验证了判别器分数 $S_{\ast}$ 对于策略熵的预测能力：

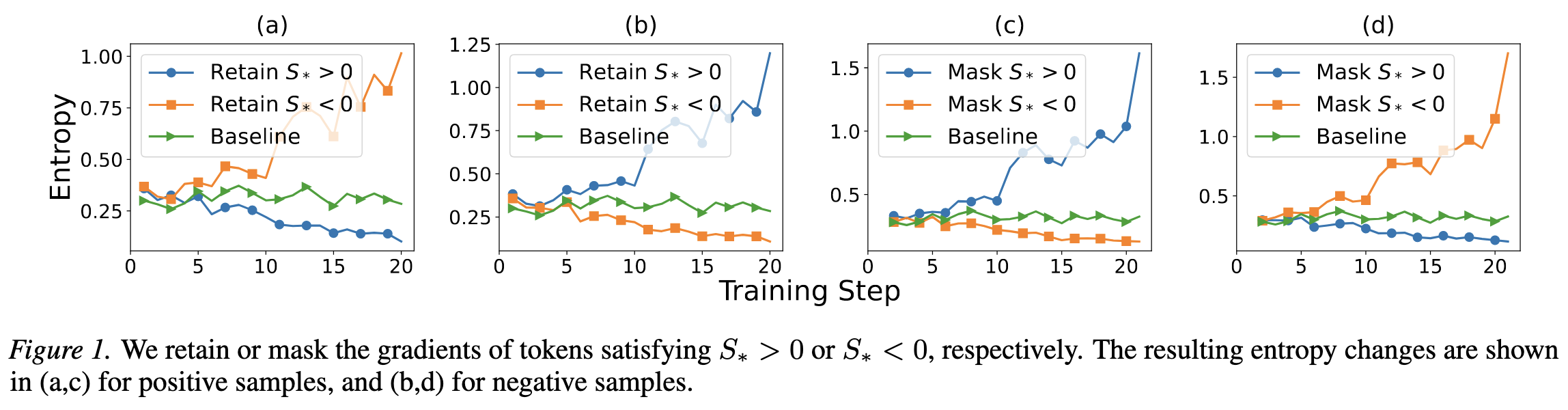
EntDynamic_1

只留下 $S_{\ast}\gt 0$ 的token，熵显著增加
只留下 $S_{\ast}\lt 0$ 的token，熵显著减少

这与理论预测完全一致。

4.3. Clip-B和Clip-V对熵的影响

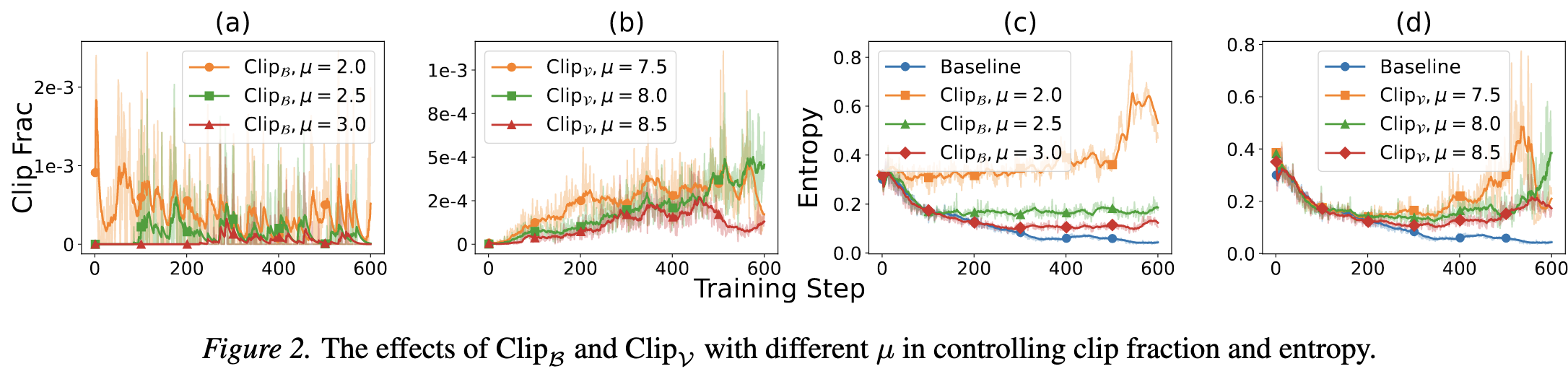
EntDynamic_2

可以看到，当 $\mu$ 越小，表示Clip的约束力度越大，此时熵会更高。

Appendix

Apd.1. Proof of Lemma 1

下面我们来证明 Lemma 1 \eqref{eq:lemma-1}。

对策略分布变化量 $\Delta\pi_i$ 进行一阶泰勒展开得：

\[\begin{equation} \Delta\pi_i=\sum_{j=1}^{V}\frac{\partial \pi_i}{\partial z_j}\Delta z_j+O(\varepsilon^2) \end{equation}\]

其中，$\forall j\in[V]$，有：

\[\begin{equation} \begin{aligned} \frac{\partial \pi_i}{\partial z_j} &=\frac{\partial }{\partial z_j}\text{softmax}(z_i)\\ &=\pi_i\cdot\left( \mathbb{I}(i=j)-\pi_j \right)\\ \Delta z_j &=\varepsilon\cdot \mathbb{I}(j=k) \end{aligned} \end{equation}\]

代入得：

\[\begin{equation} \begin{aligned} \Delta\pi_i &=\frac{\partial \pi_i}{\partial z_k}\cdot\varepsilon\\ &=\varepsilon\cdot \pi_i\cdot\left( \mathbb{I}(i=k)-\pi_k \right)\\ &= \begin{cases} \varepsilon\pi_k(1-\pi_k), & i=k\\ -\varepsilon\pi_k\pi_i, & i\neq k \end{cases} \end{aligned} \end{equation}\]

得证。

Apd.2. Proof of Theorem 1

下面我们来证明 Theorem 1 \eqref{eq:theorem-1}。

得证。

Apd.3. Proof of Theorem 2

下面我们来证明 Theorem 2 \eqref{eq:theorem-2}。

首先我们来计算策略分布的变化量：

\[\begin{equation} \begin{aligned} \Delta \pi &=\frac{\partial \pi}{\partial z}\Delta z\\ &=\left(\text{diag}(\pi)-\pi\pi^T\right)\alpha(e_k-\pi)\\ &=\alpha\left[ \pi\odot(e_k-\pi) -\pi\left(\pi_k-\Vert\pi\Vert^2\right) \right] \end{aligned} \end{equation}\]

对于某一个分量 $\pi_i$，其改变量则可以写为：

\[\begin{equation} \Delta \pi_i=\alpha\left[ \pi_i(\mathbb{I}(i=k)-\pi_i) -\pi_i\left(\pi_k-\Vert\pi\Vert^2\right) \right] \end{equation}\]

复用 \eqref{eq:proof-theorem-1} 中的结果：

\[\begin{equation} \begin{aligned} \Delta\mathcal{H} &=\mathcal{H}(\pi+\Delta\pi)-\mathcal{H}(\pi)\\ &=\sum_{i=1}^{V}\frac{\partial \mathcal{H}(\pi)}{\partial \pi_i}\Delta \pi_i+O(\Vert\Delta\pi\Vert^2)\\ &=-\sum_{i=1}^{V}(1+\log\pi_i)\Delta \pi_i+O(\alpha^2)\\ &=-\sum_{i=1}^{V}\Delta \pi_i\log\pi_i+O(\alpha^2)\\ &= -\alpha \sum_{i=1}^{V}\log\pi_i\left[ \pi_i(\mathbb{I}(i=k)-\pi_i) -\pi_i\left(\pi_k-\Vert\pi\Vert^2\right) \right] +O(\alpha^2)\\ &= -\alpha \left[\sum_{i=1}^{V} \pi_i\log\pi_i(\mathbb{I}(i=k)-\pi_i) -\sum_{i=1}^{V}\pi_i\log\pi_i(\pi_k-\Vert\pi\Vert^2) \right] +O(\alpha^2)\\ &= -\alpha \left[ \pi_k\log\pi_k(1-\pi_k) -\sum_{i\neq k} \pi_i^2\log\pi_i +(\pi_k-\Vert\pi\Vert^2)\mathcal{H}(\pi) \right] +O(\alpha^2)\\ &= -\alpha \left[ \pi_k(\log\pi_k+\mathcal{H}(\pi))-\left(\pi_k^2\log\pi_k +\sum_{i\neq k} \pi_i^2\log\pi_i +\mathcal{H}(\pi)\Vert\pi\Vert^2\right) \right] +O(\alpha^2)\\ &= -\alpha \left[ S_{\ast} -\left( \sum_{i=1}^{V}\pi_i^2\log\pi_i +\mathcal{H}(\pi)\sum_{i=1}^{V}\pi_i^2 \right) \right] +O(\alpha^2)\\ &= -\alpha \left[ S_{\ast} -\left( \sum_{i=1}^{V}\pi_i^2\left(\log\pi_i+\mathcal{H}(\pi)\right) \right) \right] +O(\alpha^2)\\ \end{aligned} \end{equation}\]

其中，

\[\begin{equation} \begin{aligned} \mathbb{E}_{i\sim \pi}\left[ S_i\right] &=\sum_{i=1}^{V}\pi_i S_i\\ &=\sum_{i=1}^{V}\pi_i^2(\mathcal{H}(\pi)+\log\pi_i) \end{aligned} \end{equation}\]

因此，

\[\begin{equation} \Delta\mathcal{H}= -\alpha \left( S_{\ast}-\mathbb{E}_{i\sim \pi}\left[ S_i\right] \right) +O(\alpha^2) \end{equation}\]

定理2 \eqref{eq:theorem-2} 得证。

阅读原文

On the Entropy Dynamics in Reinforcement Fine-Tuning of Large Language Models