引言
在2026年的春节假期,我决定开始入门随机过程这门课程。这一系列博客用来记录我学习随机过程的笔记。
主要的动机其实是看到了quant的面经中无处不在的鞅、布朗运动等名词,而我本身自己的研究也大量涉及到随机过程中的概念和结论,因此决定系统地学习一下随机过程。
其实说来惭愧,我研究生是选了这门课的,但是第一节课被概率论给劝退了,毕竟大家都说随机过程随机过。
我主要是跟着张颢老师在国科大的课程录像来学习(这个录像很有名,在B站一搜就是),我自己也买了一本张颢老师推荐的 “Probability, Random Variable and Stochastic Process” 这本书,用作一些概率论背景的补充。
一、随机过程学习什么
在概率论中,我们使用随机变量 (Random Variable) 来刻画随机事件。具体来说,一个随机变量是一个函数 $X: \Omega \to \mathbb{R}$,它将样本空间中的每个元素映射到实数域上。对于一个随机变量,我们可以有各种各样的刻画,比如说:
- 分布函数:$F(x) = P(X \leq x)$ 描述了随机变量 $X$ 小于等于 $x$ 的概率。
- 概率密度:$f(x) = \frac{\mathrm{d}F(x)}{\mathrm{d}x}$ 描述了随机变量 $X$ 在 $x$ 处的变化率。
- 期望:$\mathbb{E}[X] = \int_{\Omega} x f(x) \mathrm{d}x$ 描述了随机变量 $X$ 的平均取值。
- 方差:$\text{Var}[X] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2$ 描述了随机变量 $X$ 的取值离散程度。
- $k$ 阶矩:$\mathbb{E}[X^k] = \int_{\Omega} x^k f(x) \mathrm{d}x$
随机过程主要研究的是 多个随机变量 之间的关系,关注随机变量之间的关联关系。
在本系列中,我们主要学习三种关联方式:
- 线性相关:包括线性相关的时域和频域特征,最后我们将研究一个非常重要的随机过程:高斯过程。
- 马尔可夫性:包括离散时间、连续时间的马尔可夫性,并学习一个最简单的马尔可夫过程:泊松过程。
- 鞅:主要介绍鞅在金融数学中的应用。
二、线性相关 (Linear Correlation)
线性相关考察的是两个随机变量 $X$ 和 $Y$ 之间的关联,即是一种二元关系 (Binary Relation)。
2.1. 两个随机变量之间的关系
我们首先通过举一些例子来大致了解一下我们如何刻画两个随机变量之间的关系。
对于两个随机变量 $X$ 和 $Y$,其联合分布 $f_{X,Y}(x,y)$ 在二维平面上可能有以下几种类型:
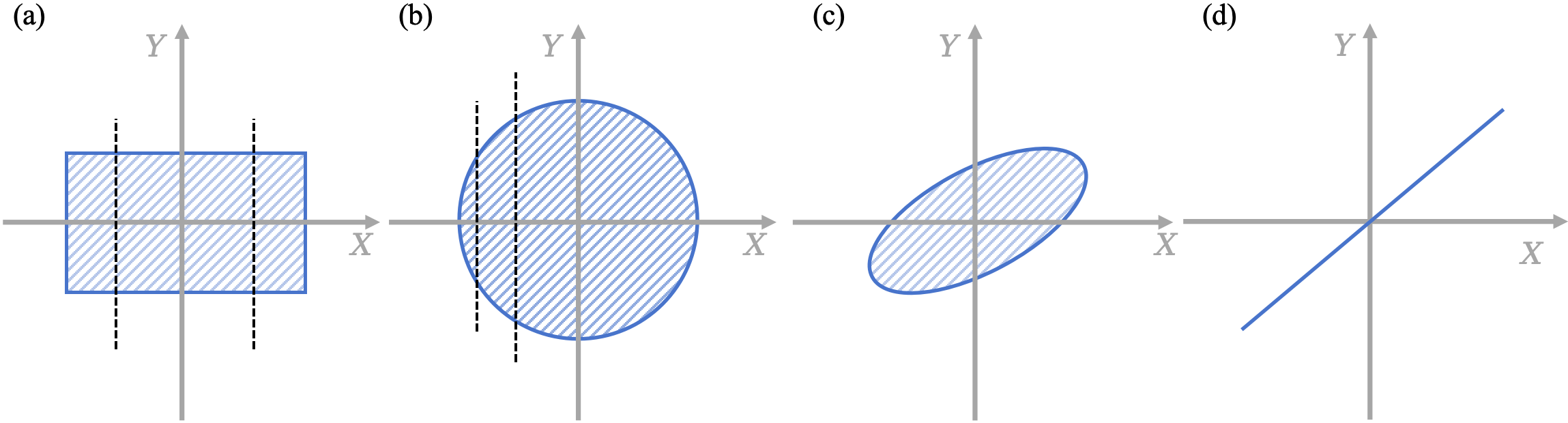
Case 1. 矩形分布
我们考察这两个随机变量的关系时,往往可以先固定住其中一个随机变量,然后考虑另一个随机变量的的分布。
在 Fig. 1(a) 中我们可以看到,无论随机变量 $X$ 取何值,随机变量 $Y$ 的分布都是相同的。也就是说,这两个随机变量之间没有任何关系。
因此,如果两个随机变量 $X$ 和 $Y$ 的联合分布呈现 如 Fig. 1(a) 所示的形状,那么我们称这两个随机变量是 相互独立 的 (Independent)。
Case 2. 圆形分布
应用同样的方法在如 Fig. 1(b) 中我们可以看到,当等高线是一个圆形时,两个随机变量之间就存在某种关系了,即 $Y$ 的分布是依赖于 $X$。
然而,我们现在不能用明确的语言来表述:当 $X$ 变化时,$Y$ 的分布会发生什么变化。但是,我们仍然可以找到一些规律性。比如说,我们可以看到,无论 $X$ 如何变化,都有 $Y$ 的均值 $\mathbb{E}[Y]=0$。
Case 3. 椭圆分布
如果我们的联合分布呈现出如 Fig. 1(c) 所示的形状,我们不难发现,二者不仅不独立,均值 $\mathbb{E}[Y]$ 也是依赖于 $X$ 的。但我们仍然可以有一些定性的分析。比如说当 $X$ 增大时,$Y$ 也在随之增大。
当然,我们不能够说这两个随机变量之间就是直接的线性关系,因为椭圆中间是有宽度的。但我们能够隐约地认识到,当这个宽度越来越小时,二者的线性关系就会越来越强。在两种极限情况下:
2.2. 符号语言定义
对于两个随机变量 $X$ 和 $Y$,我们希望寻找 $Y$ 和 $kX$ 之间的关系,我们就需要一个度量来衡量二者之间的距离。在这里我们采用平方距离 $\sqrt{\mathbb{E}[(Y-kX)^2]}$。
我们有:
\[\begin{equation} \begin{aligned} \mathbb{E}[(Y-kX)^2] &=\mathbb{E}[Y^2]+k^2\mathbb{E}[X^2]-2k\mathbb{E}[XY]\\ \end{aligned} \end{equation}\]我们关注的是交叉项 $\mathbb{E}[XY]$,这也是两个随机变量之间的相关性计算方式。由于这个交叉项是内积的形式,因此我们可以从几何的视角来看待两个随机变量,即两个随机变量也存在诸如正交性之类的概念。
关于随机变量之间的相关,我们有以下重要的观点。
Remark 1. (独立与不相关)
如果我们称两个随机变量是【不相关】(Uncorrelated),我们实际上是在说这两者是【正交】(Orthogonal) 的,即 $\mathbb{E}[XY]=0$。
Note:有些书上会把不相关定义为 $\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$,其实这两种定义在某种程度上是等价的。因为我们只需要分别对 $X$ 和 $Y$ 进行中心化,即变为 $X-\mathbb{E}[X]$ 和 $Y-\mathbb{E}[Y]$,那么这二者就是等价的。 换句话讲,我们用正交来描述不相关,相当于是做了某种意义的中心化。 因此,在后文中我们对这两种方式不作具体区分,都可以称之为不相关。
因此,我们可以说:独立一定不相关。但是反过来却不一定成立,下面是一个经典的反例。
设 $\Theta\sim U[0,2\pi]$,定义 $X=\cos\Theta$,$Y=\sin\Theta$。显然,这两个随机变量不独立,因为这两个随机变量满足 $X^2+Y^2=1$。但另一方面,这两个随机变量却是不相关的。
我们考察 $X$ 和 $Y$ 的期望:
\[\begin{equation} \begin{aligned} \mathbb{E}[X] &= \int_{-\infty}^{\infty}\cos\theta f_{\Theta}(\theta)\mathrm{d}\theta \\ &= \int_{0}^{2\pi}\cos\theta\frac{1}{2\pi}\mathrm{d}\theta \\ &= 0 \end{aligned} \end{equation}\]同理我们也可以得出 $\mathbb{E}[Y]=0$。
我们再考虑 $XY$ 的期望:
\[\begin{equation} \begin{aligned} \mathbb{E}[XY] &= \int_{0}^{2\pi}\cos\theta\sin\theta\frac{1}{2\pi}\mathrm{d}\theta \\ &= \frac{1}{2\pi}\int_{0}^{2\pi}\sin\theta\mathrm{d}\sin\theta \\ &= 0 \end{aligned} \end{equation}\]因此,我们有 $\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]=0$,即二者是不相关的。
Remark 2. (相关的柯西不等式)
我们有:
\[\begin{equation} \lvert\mathbb{E}(XY)\rvert\le\sqrt{\mathbb{E}[X^2]\mathbb{E}[Y^2]} \label{eq:correlation-cauchy-inequality} \end{equation}\]公式 \eqref{eq:correlation-cauchy-inequality} 被称为柯西不等式,其证明在附录1中。
Remark 3. (多个随机变量的相关性)
设 $X=(X_1,X_2,\dots,X_n)^T$,其中每个分量 $X_i$ 都是一个随机变量。我们希望考虑这个 $X$ 的每一个分量之间的相关性,我们就需要考虑 $\binom{n}{2}=\frac{n(n-1)}{2}$ 个分量对之间的相关性。此时,我们就需要引入一个相关矩阵 (Correlation Matrix),来描述这些相关性。
我们定义相关矩阵为 $R_X:=\mathbb{E}[XX^T]$,其中,$R_X(i,j)=\mathbb{E}[X_iX_j]$。
首先我们可以发现,相关矩阵 $R_X$ 是一个对称矩阵,因为 $\mathbb{E}[X_iX_j]=\mathbb{E}[X_jX_i]$。
其次,这个矩阵还是半正定的,即 $\forall z,z^TR_Xz\ge0$:
\[\begin{equation} \begin{aligned} z^TR_Xz &=z^T\mathbb{E}[XX^T]z\\ &=\underbrace{\mathbb{E}[z^TXX^Tz]}_{z不是随机变量}\\ &=\underbrace{\left(\mathbb{E}[X^Tz]\right)^2}_{X^Tz是标量}\\ &\ge0 \end{aligned} \end{equation}\]Appendix
Apd.1. Proof of Eq. \eqref{eq:correlation-cauchy-inequality}
我们这里证明一个更加广泛的结论,即基于内积形式的柯西不等式。由于求期望实际上也是一种内积运算,因此我们这里的结论可以推广到各种各样的场景中,包括公式 \eqref{eq:correlation-cauchy-inequality}。
内积形式的柯西不等式可以表达为:
\[\begin{equation} \langle X,Y\rangle\le\sqrt{\langle X,X\rangle\langle Y,Y\rangle} \label{eq:cauchy-inequality} \end{equation}\]考虑辅助函数 $g(\alpha)=\langle \alpha X+Y,\alpha X+Y\rangle$,根据内积的非负性,我们有 $g(\alpha)\ge0$。又由内积的双线性,我们有:
\[\begin{equation} \begin{aligned} g(\alpha) &=\langle \alpha X+Y,\alpha X+Y\rangle\\ &=\alpha^2\langle X,X\rangle+\langle Y,Y\rangle+2\alpha\langle X,Y\rangle\\ &\ge0 \end{aligned} \end{equation}\]当我们把上式看作一个关于 $\alpha$ 的二次函数时,由于其二次项系数为 $\langle X,X\rangle\ge 0$,且整个函数 $g(\alpha)\ge 0$,因此其判别式:
\[\begin{equation} \begin{aligned} \Delta &=4\langle X,Y\rangle^2-4\langle X,X\rangle\langle Y,Y\rangle\\ &\le0 \end{aligned} \end{equation}\]移项得 $\langle X,Y\rangle\le\sqrt{\langle X,X\rangle\langle Y,Y\rangle}$。公式 \eqref{eq:cauchy-inequality} 即得证。
借助公式 \eqref{eq:cauchy-inequality},我们还可以写出除了公式 \eqref{eq:correlation-cauchy-inequality} 之外的其他结论。比如说:
\[\begin{equation} \left( \sum_{k}x_ky_k \right)\le\sqrt{\sum_{k}x_k^2\sum_{k}y_k^2} \end{equation}\] \[\begin{equation} \int f(x)g(x)\mathrm{d}x\le\sqrt{\int f(x)^2\mathrm{d}x\int g(x)^2\mathrm{d}x} \end{equation}\]