随机过程(2)

一、什么是随机过程

1.1. 随机过程的定义

随机过程就是一组随机变量的集合 $X(t)$，根据 $t$ 的连续或离散性，我们就可以将随机过程分为连续随机过程和离散随机过程。

Note: $X(t)$ 中的 $t$ 只是对不同随机变量的标注，并不一定代表时间。

如果 $t$ 代表时间，那么 $X(t)$ 就是一个随机过程。

如果 $t$ 代表空间，那么 $X(t)$ 就称为随机场。

$t$ 具体代表什么物理含义并不关键，只是一个用于区分不同随机变量的标识。

当我们给定 $t$ 的值后，$X(t)$ 就变成了一个的随机变量。因此，随机过程从某种意义上可以看作是一个随机函数。因此，随机过程更严格的写法应该是 $X(\omega,t)$，其中 $\omega\in\Omega$ 是样本空间中的样本点。

同理的，当我们给定一个样本点 $\omega$，我们能够得到一组关于 $t$ 值 $X(t\mid \omega)$，我们将其称之为样本轨道 (sample path)。我们平时看到的股票价格，就可以看作是某个随机过程的一条样本轨道。

1.2. 随机过程的相关函数

把上一章中随机变量的相关这个概念用到随机过程中，我们就可以定义下面这样的相关函数 (Auto Correlation Function) 来刻画随机过程 $X(t)$ 在不同时间点 $t$ 和 $s$ 时的相关性：

\[\begin{equation} R_X(t,s):=\mathbb{E}[X(t)X(s)] \end{equation}\]

这个相关函数有着下面的一些性质：

对称性：$R_X(t,s)=R_X(s,t)$。
非负性：$R_X(t,t)\ge 0$。
柯西不等式：$\lvert R_X(t,s)\rvert \le \sqrt{R_X(t,t)R_X(s,s)}$。

二、宽平稳假设

为了更好地研究这个相关性函数，我们一般会对随机过程作出一些平稳性 (stationary) 假设。平稳性假设意味着，随机过程 $X(t)$ 的某些统计性质，如期望、方差、相关函数等，不依赖于时间点的具体取值。

在这里，我们引入第一种平稳性假设，称为【宽平稳】假设 (wide sense stationary, w.s.s.)。当我们称一个随机过程是宽平稳的，那么它会有以下两个性质：

其均值是个常数：$\forall t,\mathbb{E}[X(t)]\equiv m$。
相关函数具有时移不变性：$\forall T, R_X(t+T,s+T)=R_X(t,s)$。

2.1. 宽平稳相关函数的性质

2.1.1. 普通相关函数性质的延伸

从性质2我们可以看出，对于一个宽平稳的随机过程，其相关函数只依赖于时间点的差 $t-s$，而不依赖于时间点的具体取值。因此相关函数就退化为一个一元函数 $R_X(t-s)$，能够比较好地进行研究和应用。

因此，在宽平稳的假设下，上面描述的随机函数的三个性质可以进一步表达为：

$R_X(\tau)=R_X(-\tau)$。
$R_X(0)\ge 0$。
$\lvert R_X(\tau)\rvert \le R_X(0)$，即 $\tau=0$ 是相关函数的最大值。

注意，这里的 $\tau$ 是时间点的差，而不是具体的时间点。因此，这三个性质其实是符合我们对相关函数的直观想象的。因为当时间差越大，随机变量之间的相关性就越小。

除了以上的三个性质，宽平稳相关函数还有以下的重要性质。

2.1.2. 周期性

对于一个宽平稳的随机过程 $X(t)$，假如其相关函数满足 $R_X(0)=R_X(T)$，则一定有 $R_X(T+\tau)=R_X(\tau)$。

这个结论其实很有意思。我们在前面已经知道，$R_X(0)$ 是相关函数的一个最大值。这个结论又告诉我们，如果在某一个点 $T$ 上也能取到最大值，那么这个相关函数一定是以 $T$ 为周期的周期函数。

这也就是说，相关函数的一些局部性质能够影响到其全局的性质。

下面我们来证明这个结论。我们的证明路线如下：

\[\begin{equation} R_X(0)=R_X(T) \overset{①}{\implies} \mathbb{E}\lvert X(t)-X(t+T)\rvert^2=0 \overset{②}{\implies} R_X(T+\tau)=R_X(\tau) \end{equation}\]

我们首先证明 $①$：

\[\begin{equation} \begin{aligned} \mathbb{E}\lvert X(t)-X(t+T)\rvert^2 &= \mathbb{E}\left[X(t)^2\right]+\mathbb{E}\left[X(t+T)^2\right]-2\mathbb{E}\left[X(t)X(t+T)\right] \\ &= R_X(t-t)+R_X((t+T)-(t+T))-2R_X(t+T-t) \\ &= R_X(0)+R_X(0)-2R_X(T) \\ &= 0 \\ \label{eq:circ1} \end{aligned} \end{equation}\]

然后我们证明 $②$：

\[\begin{equation} \begin{aligned} \lvert R_X(\tau)-R_X(\tau+T)\rvert &=\left\lvert \mathbb{E}[X(0)X(\tau)] - \mathbb{E}[X(0)X(\tau+T)]\right\rvert \\ &= \underbrace{\left\lvert \mathbb{E}\left[ X(0)(X(\tau)-X(\tau+T)) \right] \right\rvert}_{\text{Jensen Inequality}} \\ &\le \underbrace{\mathbb{E}\left[ \lvert X(0) \rvert\cdot\lvert X(\tau)-X(\tau+T) \rvert \right]}_{\text{Cauchy Inequality}} \\ &\le \left[\mathbb{E}\left[ \lvert X(0) \rvert^2\right] \cdot \underbrace{\mathbb{E}\left[\lvert X(\tau)-X(\tau+T) \rvert^2 \right]}_{①}\right]^{\frac{1}{2}} \\ &=0\\ \label{eq:circ2} \end{aligned} \end{equation}\]

因此，$R_X(\tau)-R_X(\tau+T)=0$，得证。

2.1.3. 连续性

对于一个宽平稳的随机过程 $X(t)$，假如其相关函数 $R_X(\tau)$ 在 $\tau=0$ 是连续的，则 $R_X(\tau)$ 处处连续。

下面我们来证明这一点。

由于 $R_X(\tau)$ 在 $\tau=0$ 是连续的，因此我们有：

\[\begin{equation} \lim_{h\to 0} R_X(h)=R_X(0) \end{equation}\]

复用公式 $\eqref{eq:circ1}$，我们有：

\[\begin{equation} \begin{aligned} \lim_{h\to 0}\mathbb{E}\lvert X(t+h)-X(t)\rvert^2 &= \lim_{h\to 0}\mathbb{E}\left[X(t+h)^2\right]+\mathbb{E}\left[X(t)^2\right]-2\mathbb{E}\left[X(t+h)X(t)\right] \\ &= \lim_{h\to 0}2R_X(0)-2R_X(h) \\ &=0 \end{aligned} \end{equation}\]

考虑任意点 $\tau_0$，复用 \eqref{eq:circ2} 得：

\[\begin{equation} \begin{aligned} \lim_{h\to 0}\lvert R_X(\tau_0+h)-R_X(\tau_0)\rvert &=\lim_{h\to 0}\left\lvert \mathbb{E}[X(t)X(t+\tau_0+h)] - \mathbb{E}[X(t)X(t+\tau_0)]\right\rvert \\ &= \lim_{h\to 0}\left\lvert \mathbb{E}\left[ X(t)(X(t+\tau_0+h)-X(t+\tau_0)) \right] \right\rvert \\ &\le \lim_{h\to 0}\mathbb{E}\left[ \lvert X(t) \rvert\cdot\lvert X(t+\tau_0+h)-X(t+\tau_0) \rvert \right] \\ &\le \lim_{h\to 0}\sqrt{\mathbb{E}\left[ \lvert X(t) \rvert^2\right] \cdot \mathbb{E}\left[\lvert X(t+\tau_0+h)-X(t+\tau_0) \rvert^2 \right]} \\ &=0\\ \end{aligned} \end{equation}\]

得证。

2.1.4. 正定性

首先我们定义函数的正定性。我们称一个函数 $f(x)$ 是正定函数 (Positive Definite Function)，当且仅当 $\forall n,\forall x_1,\dots,x_n$，矩阵 $\lbrace f(x_i-x_j)\rbrace_{i,j=1}^n$ 是正定矩阵。

下面我们将证明，宽平稳随机过程的相关函数是正定函数。

回顾相关矩阵和相关函数的定义，我们知道相关矩阵的第 $i$ 行第 $j$ 列的元素 $R_X(i-j)$ 就是相关函数 $R_X(t_i-t_j)=\mathbb{E}[X(t_i)X(t_j)]$。令 $X=(X(t_1),X(t_2),\dots,X(t_n))^T$，则相关矩阵就可以写成 $R_X=\mathbb{E}[XX^T]$，且在上一篇中我们已经证明了相关矩阵的正定性。

因此，相关函数 $R_X(\tau)$ 是正定函数。

实际上，这个结论是双向的。也就是说，给定一个正定函数，我们都可以唯一地构造一个随机过程（证明略），使其相关函数就是这个正定函数，即【相关函数和正定函数是一一对应的】。

2.1.4.1. Bochner’s Theorem

当我们需要判断一个函数的正定性时，使用定义来证明是非常困难的。这个时候，我们有一个非常有用的定理来帮助我们，就是下面介绍的Bochner定理。

Theorem 1. (Bochner) 一个函数 $f(x)$ 是正定的，当且仅当它的傅里叶变换非负：

\[\begin{equation} \int_{-\infty}^{\infty}f(x)\exp(-j\omega x)\mathrm{d}x\ge 0 \end{equation}\]

Bochner定理的证明较为复杂，我们放在附录1中进行展示。

借由Bochner定理，我们可以非常轻松地判断一个函数是否是正定函数，也就能判断是否是某个随机过程的相关函数。

比如说，对于矩形框函数：

\[\begin{equation} \text{rect}_T(t)= \begin{cases} 1,&\lvert t\rvert \lt \frac{T}{2}\\ 0,&\text{otherwise} \end{cases} \end{equation}\]

其傅里叶变换为sinc函数：

\[\begin{equation} \begin{aligned} \mathcal{F}(\omega) &=T\text{sinc}\left(\frac{\omega T}{2}\right)\\ &=T\frac{\sin(\omega T/2)}{\omega T/2} \end{aligned} \end{equation}\]

存在负值，因此不是一个相关函数。

相反，三角框函数是两个矩形框的卷积：

\[\begin{equation} \begin{aligned} \Lambda_T(t) &= \frac{1}{T}[\text{rect}_T\circledast\text{rect}_T](t)\\ &=\begin{cases} 1-\frac{\lvert t\rvert}{T},&\lvert t\rvert \lt T\\ 0,&\text{otherwise} \end{cases} \end{aligned} \end{equation}\]

其傅里叶变换一定非负：

\[\begin{equation} \begin{aligned} \mathcal{F}(\omega) &=T\text{sinc}^2\left(\frac{\omega T}{2}\right)\\ \end{aligned} \end{equation}\]

因此，三角函数是一个相关函数。

2.2. 宽平稳随机过程举例

Case 1. 调制信号 (Modulated Signal)

我们希望考察下面的调制信号的宽平稳性质：

\[\begin{equation} X(t)=A(t)\cos(2\pi ft+\Theta) \end{equation}\]

其中，$A(t)$ 是一个w.s.s.的随机过程，$\Theta\sim U(0,2\pi)$ 独立于 $A(t)$。

首先我们考察均值

\[\begin{equation} \begin{aligned} \mathbb{E}[X(t)] &= \mathbb{E}[A(t)\cos(2\pi ft+\Theta)] \\ &= \mathbb{E}[A(t)]\cdot\underbrace{\mathbb{E}[\cos(2\pi ft+\Theta)]}_{=\int_{0}^{2\pi}\cos(2\pi ft+\theta)\mathrm{d}\theta=0} \\ &= 0 \end{aligned} \end{equation}\]

然后我们考察时移不变性

\[\begin{equation} \begin{aligned} R_X(t,s) &= \mathbb{E}[A(t)\cos(2\pi ft+\Theta)\cdot A(s)\cos(2\pi fs+\Theta)] \\ &= \mathbb{E}[A(t)A(s)]\cdot\mathbb{E}[\cos(2\pi ft+\Theta)\cos(2\pi fs+\Theta)] \end{aligned} \end{equation}\]

由于 $A(t)$ 是一个 w.s.s. 的随机过程，因此 $\mathbb{E}[A(t)A(s)]=R_A(t-s)$。

对于第二项，我们可以化简得到：

\[\begin{equation} \begin{aligned} \mathbb{E}[\cos(2\pi ft+\Theta)\cos(2\pi fs+\Theta)] &= \frac{1}{2\pi}\int_{0}^{2\pi}\underbrace{\cos(2\pi ft+\theta)\cos(2\pi fs+\theta)}_{积化和差}\mathrm{d}\theta \\ &= \frac{1}{4\pi}\left[\int_{0}^{2\pi}\underbrace{\cos(2\pi f(t-s))}_{\text{constant}}\mathrm{d}\theta\right.\\ &\quad\qquad+\left.\underbrace{\int_{0}^{2\pi}\cos(2\pi f(t+s)+2\theta)\mathrm{d}\theta}_{=0}\right] \\ &=\frac{1}{2}\cos(2\pi f(t-s)) \end{aligned} \end{equation}\]

因此，原式可以化简为：

\[\begin{equation} \begin{aligned} R_X(t,s) &= \mathbb{E}[A(t)A(s)]\cdot\mathbb{E}[\cos(2\pi ft+\Theta)\cos(2\pi fs+\Theta)]\\ &= R_A(t-s)\cdot\frac{1}{2}\cos(2\pi f(t-s))\\ \end{aligned} \end{equation}\]

因此，$R_X(t,s)$ 也只依赖于于时间差 $t-s$。综上所述，$X(t)$ 也是一个w.s.s.的随机过程。

Case 2. 随机电报信号 (Random Telegraph Signal)

随机电报信号是一种特殊的随机过程，它的取值只有 $+1$ 和 $-1$ 两种可能。

假设在一段时间 $s$ 内，随机电报信号 $X(t)$ 跳变的次数 $N(s)$ 是一个服从 Poisson 分布的随机变量，即 $N(s)\sim Pois(\lambda s)$，其中 $\lambda$ 是一个常数，称为跳变率 (jump rate)：

\[\begin{equation} P(N(s)=k) = \frac{(\lambda s)^k}{k!}\exp(-\lambda s) \end{equation}\]

又假设 $X(0)$ 服从伯努利分布，即：

\[\begin{equation} X(0) \sim \begin{pmatrix} 1&-1\\\frac{1}{2}&\frac{1}{2} \end{pmatrix} \end{equation}\]

下面我们来考察 $X(t)$ 的宽平稳性质。

首先我们考虑其均值

\[\begin{equation} \begin{aligned} \mathbb{E}[X(t)] &= \sum_{k\in\{+1,-1\}}kP(X(t)=k) \\ &= P(X(t)=+1) - P(X(t)=-1) \end{aligned} \end{equation}\]

根据全概率公式：

\[\begin{equation} \begin{aligned} P(X(t)=1) &= P(X(t)=1\mid X(0)=-1)P(X(0)=-1) \\ &\quad+ P(X(t)=1\mid X(0)=1)P(X(0)=1) \\ &= \frac{1}{2}\left(P(X(t)=1\mid X(0)=-1)+P(X(t)=1\mid X(0)=1)\right)\\ \label{eq:total} \end{aligned} \end{equation}\]

其中，$P(X(t)=1\mid X(0)=-1)$ 表示在 $s=t-0=t$ 这段时间内，信号跳变的次数 $N(t)$ 为奇数的概率：

\[\begin{equation} \begin{aligned} P(X(t)=1\mid X(0)=-1) &= P(N(t) \text{ is odd}) \\ &= \sum_{k \text{ is odd}} P(N(t)=k) \\ &= \sum_{k \text{ is odd}} \frac{(\lambda t)^k}{k!}\exp(-\lambda t) \\ \label{eq:odd} \end{aligned} \end{equation}\]

这里引入一个小技巧，我们分别将 $\exp(\lambda t)$ 和 $\exp(-\lambda t)$ 进行泰勒展开得：

\[\begin{equation} \begin{aligned} \exp(\lambda t) &= \sum_{k=0}^{\infty}\frac{(\lambda t)^k}{k!} \\ \exp(-\lambda t) &= \sum_{k=0}^{\infty}(-1)^k\frac{(\lambda t)^k}{k!}\\ \label{eq:taylor} \end{aligned} \end{equation}\]

这里的 $k$ 取到全体自然数，但公式 \eqref{eq:odd} 中只涉及到了奇数项，因此可以将公式 \eqref{eq:taylor} 的上式减下式，就能够消除所有的偶数项，即

\[\begin{equation} \sum_{k \text{ is odd}} \frac{(\lambda t)^k}{k!}=\frac{1}{2}\left(\exp(\lambda t)-\exp(-\lambda t)\right) \end{equation}\]

带入公式 \eqref{eq:odd} 中，我们有：

\[\begin{equation} \begin{aligned} P(X(t)=1\mid X(0)=-1) &= \sum_{k \text{ is odd}} \frac{(\lambda t)^k}{k!}\exp(-\lambda t) \\ &= \frac{1}{2}\left(\exp(\lambda t)-\exp(-\lambda t)\right)\exp(-\lambda t) \\ &=\frac{1-\exp(-2\lambda t)}{2} \end{aligned} \end{equation}\]

同理，我们有：

\[\begin{equation} \begin{aligned} P(X(t)=1\mid X(0)=1) &= \sum_{k \text{ is even}} \frac{(\lambda t)^k}{k!}\exp(-\lambda t) \\ &= \frac{1}{2}\left(\exp(\lambda t)+\exp(-\lambda t)\right)\exp(-\lambda t) \\ &=\frac{1+\exp(-2\lambda t)}{2}\\ \label{eq:even} \end{aligned} \end{equation}\]

Note：从上面两个结果我们可以看出，一个服从泊松分布的随机变量是奇数和偶数的概率居然是不一样的。当 $t$ 比较小时，偶数的概率更大。当 $t$ 逐渐增大时，奇偶的概率趋于一致。这还是比较奇妙的。

把上面两个结果代入公式 \eqref{eq:total} 中，我们有：

\[\begin{equation} \begin{aligned} P(X(t)=1) &= \frac{1}{2}\left(P(X(t)=1\mid X(0)=-1)+P(X(t)=1\mid X(0)=1)\right) \\ &= \frac{1}{2}\left(\frac{1-\exp(-2\lambda t)}{2}+\frac{1+\exp(-2\lambda t)}{2}\right) \\ &= \frac{1}{2} \end{aligned} \end{equation}\]

又因为 $P(X(t)=-1)=1-P(X(t)=1)=\frac{1}{2}$，因此 $X(t)$ 的期望 $ \mathbb{E}[X(t)]=0$。

然后我们考察时移不变性

考虑 $X(t)$ 的相关函数：

\[\begin{equation} \begin{aligned} R_X(t,s) &= \mathbb{E}[X(t)X(s)] \\ &= P(X(t)X(s)=1)-P(X(t)X(s)=-1) \\ \label{eq:corr} \end{aligned} \end{equation}\]

我们先假设 $t\geq s$。经过上面的分析，我们已经知道 $P(X(t)X(s)=1)$ 表示从 $s$ 到 $t$ 这段时间内，信号跳变的次数为偶数的概率，这个结果我们在公式 \eqref{eq:even} 中已经计算过了，即：

\[\begin{equation} \begin{aligned} P(X(t)X(s)=1) &= P(N(t-s) \text{ is odd}) \\ &= \frac{1+\exp(-2\lambda(t-s))}{2} \\ \end{aligned} \end{equation}\]

同理，

\[\begin{equation} \begin{aligned} P(X(t)X(s)=-1) &= P(N(t-s) \text{ is even}) \\ &= \frac{1-\exp(-2\lambda(t-s))}{2} \\ \end{aligned} \end{equation}\]

代回公式 \eqref{eq:corr} 中，我们有：

\[\begin{equation} \begin{aligned} R_X(t,s) &= P(X(t)X(s)=1)-P(X(t)X(s)=-1) \\ &= \frac{1+\exp(-2\lambda(t-s))}{2}-\frac{1-\exp(-2\lambda(t-s))}{2} \\ &= \exp(-2\lambda(t-s)) \\ \end{aligned} \end{equation}\]

这里发现 $R_X(\tau)=\exp(-2\lambda\tau)$ 并非一个偶函数，不符合宽平稳相关函数的性质。这是因为我们假设了 $t\geq s$。因此，真正的相关函数应该是：

\[\begin{equation} R_X(t,s)=\exp(-2\lambda\lvert t-s\rvert) \\ \end{equation}\]

综上所述，$R_X(t,s)$ 只与 $t-s$ 有关，因此 $X(t)$ 是时移不变的，是一个宽平稳随机过程。

三、从频域分析随机过程

在Bochner定理中，我们已经初步尝试了从频域的角度来分析一个随机过程的性质。

3.1. 确定性函数的傅里叶分析

首先我们回顾一下，在确定性函数中我们是怎么导出傅里叶变换的。我们将从周期函数入手，然后推广到非周期函数。

3.1.1. 周期函数

对于一个周期函数，它满足 $\exists T>0, X(t)=X(t+T)$，我们可以对他进行下面的傅里叶展开，得到其【傅里叶级数】(Fourier Series)：

\[\begin{equation} X(t)=\sum_{k}\alpha_k\exp(j\omega_k t) \end{equation}\]

其中，$\omega_k=2\pi k/T$。我们一般把 $2\pi/T$ 称为基频，基频的整数倍称为倍频。

系数 $\alpha_k$ 是在一个周期上 $X(t)$ 和 $\exp(-j\omega_k t)$ 的内积：

\[\begin{equation} \alpha_k=\frac{1}{T}\int_{-T/2}^{T/2}X(t)\exp(-j\omega_k t)\mathrm{d}t \end{equation}\]

对于非周期函数，我们也可以将其进行周期延拓之后展开为傅里叶级数。

3.1.2. 非周期函数

我们定义非周期函数为周期 $T\to\infty$ 的函数。

我们先把 $\alpha_k$ 代入傅里叶级数中得到：

\[\begin{equation} X(t)=\sum_{k}\frac{1}{T}\left(\int_{-T/2}^{T/2}X(s)\exp(-j\omega_k s)\mathrm{d}s\right)\exp(j\omega_k t) \end{equation}\]

当 $T\to\infty$ 时，$2\pi/T\to 0$，即 $\omega_k$ 之间的间距在不断减小，就相当于我们把区间 $[-T/2,T/2]$ 无限细分，每个小区间的宽度都在不断减小。在极限情况下，上面的求和就变成了积分。

这里有一个细节。由于我们划分的区间长度为 $2\pi/T$，因此极限和前面的分母应该是 $2\pi/T$，此时只有 $1/T$，因此要变为下面的形式：

\[\begin{equation} X(t)=\frac{1}{2\pi}\sum_{k}\frac{2\pi}{T}\left(\int_{-T/2}^{T/2}X(s)\exp(-j\omega_k s)\mathrm{d}s\right)\exp(j\omega_k t) \label{eq:fourier-series} \end{equation}\]

Note：这也就是为什么傅里叶反变换 \eqref{eq:inv_fourier} 有个系数 $1/2\pi$。

对上式进行连续化之后，就变为：

\[\begin{equation} X(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\hat{X}(\omega)\exp(j\omega t)\mathrm{d}\omega \label{eq:fourier-transform} \end{equation}\]

其中，

\[\begin{equation} \hat{X}(\omega)=\int_{-\infty}^{\infty}X(s)\exp(-j\omega s)\mathrm{d}s \end{equation}\]

公式 \eqref{eq:fourier-transform} 就是我们无比熟悉的傅里叶变换。

3.2. 随机过程的傅里叶分析

上面的结论全部都是对确定性函数的傅里叶分析工具，我们希望在随机过程中也复用上面的结果。但实际上并没有那么简单，将傅里叶分析应用到随机过程中会遭遇到一些根本性的挑战。

3.2.1. 困难在哪？

主要的问题出在将公式 \eqref{eq:fourier-series} 连续化取极限变为公式 \eqref{eq:fourier-transform}。

连续化可行的前提是 $\alpha_k$ 中的傅里叶变换要收敛，而傅里叶变换收敛的充要条件是 $X(t)$【绝对可积】，即：

\[\begin{equation} \int_{-\infty}^{\infty}\left\lvert X(t)\right\rvert\mathrm{d}t<\infty \end{equation}\]

对于一个绝对可积的函数，它需要表现出比较明显的下降收敛的趋势。但是这和随机过程的【平稳性】产生了本质的冲突。

随机过程的平稳是指随机变量的性质不会随着时间推移而变化，在上面提到的两个例子（调制信号和随机电报信号）中，我们都可以看到随机过程表现出比较平稳的特性，只有相关函数才会表现出收敛的特性（离得越远相关性越弱）。

换句话讲，当我们对随机过程进行傅里叶分析时，我们会发现：

\[\begin{equation} \int_{-\infty}^{\infty}X(t)\exp(-j\omega t)\mathrm{d}t \end{equation}\]

经常是发散的。

3.2.2. Wiener-Khintchine Theorem

在这一小节中我们将介绍 Wiener-Khintchine Theorem，它是随机过程傅里叶分析的一个重要结论。它表明：一个平稳信号的功率谱和其相关函数是一对傅里叶变换。下面我们接着上一小节的话题来说明这个结论。

虽然上面的无穷积分可能会发散，但在一个有限的区间内，其收敛性是可以保证的，这也被称为短时傅里叶变换（Short-Time Fourier Transform）：

\[\begin{equation} \int_{-\frac{T}{2}}^{\frac{T}{2}}X(t)\exp(-j\omega t)\mathrm{d}t \end{equation}\]

我们对上式进行一些操作，变为如下的形式：

\[\begin{equation} S_X(\omega)=\lim_{T\to\infty}\frac{1}{T}\mathbb{E}\left\lvert \int_{-\frac{T}{2}}^{\frac{T}{2}}X(t)\exp(-j\omega t)\mathrm{d}t\right\rvert^2 \end{equation}\]

这个变换其实是物理上的技巧，而非纯数学。比如说，求模去平方相当于是求功率，这样会把相位的信息丢掉。短时傅里叶变换本身也是很物理的一个操作。

因此，这可以看作是我们对随机信号谱特征的某种物理感觉。

我们对上式进行一些推导：

\[\begin{equation} \begin{aligned} S_X(\omega) &=\lim_{T\to\infty}\frac{1}{T}\mathbb{E}\left( \int_{-\frac{T}{2}}^{\frac{T}{2}}X(t)\exp(-j\omega t)\mathrm{d}t\right)\left( \overline{\int_{-\frac{T}{2}}^{\frac{T}{2}}X(s)\exp(-j\omega s)\mathrm{d}s}\right)\\ &=\lim_{T\to\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\int_{-\frac{T}{2}}^{\frac{T}{2}}\underbrace{\mathbb{E}\left[X(t)X(s)\right]}_{\text{w.s.s.}}\exp(-j\omega (t-s))\mathrm{d}t\mathrm{d}s\\ &=\lim_{T\to\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\int_{-\frac{T}{2}}^{\frac{T}{2}}R_X(t-s)\exp(-j\omega (t-s))\mathrm{d}t\mathrm{d}s\\ \end{aligned} \end{equation}\]

这个形式我们在Bochner定理的证明中已经出现过了（公式 \eqref{eq:variable-change}），我们就可以复用这个结果，即：

\[\begin{equation} \begin{aligned} S_X(\omega) &=\lim_{T\to\infty}\frac{1}{T}\mathbb{E}\left\lvert \int_{-\frac{T}{2}}^{\frac{T}{2}}X(t)\exp(-j\omega t)\mathrm{d}t\right\rvert^2\\ &=\int_{-\infty}^{\infty}R_X(\tau)\exp(-j\omega \tau)\mathrm{d}\tau \end{aligned} \end{equation}\]

上面这个等式非常有意思，它有很强的物理含义。等式的左侧是有量纲的，其量纲是焦耳。

因此，一个相关函数的傅里叶变换可以看作其功率谱密度 (Power Spectral Density, PSD)。功率谱的研究对象是功率，是把功率在不同频率上进行分解，其量纲是功率/频率，也就是能量。

我们把随机过程的傅里叶变换和确定性函数的傅里叶变换做一下比较。

确定性函数：直接对函数进行傅里叶变换，得到的是频谱
随机过程：对随机过程的相关函数 $R_X(\tau)$ 进行傅里叶变换，得到的是功率谱 $S_X(\omega)$

我们对 $S_X(\omega)$ 为什么是【功率谱】进行更深入的解释。

由于功率谱是把功率在频率上进行分解，因此我们可以对频率进行积分。

我们已知 $S_X(\omega)$ 的傅里叶反变换是 $R_X(\tau)$，即：

\[\begin{equation} R_X(\tau)=\frac{1}{2\pi}\int_{-\infty}^{\infty}S_X(\omega)\exp(j\omega \tau)\mathrm{d}\omega \end{equation}\]

令 $\tau=0$ 得：

\[\begin{equation} \begin{aligned} \int_{-\infty}^{\infty}S_X(\omega)\mathrm{d}\omega &=2\pi R_X(0)\\ &=2\pi\mathbb{E}\lvert X(t)\rvert^2 \end{aligned} \end{equation}\]

在随机过程中，$\mathbb{E}\lvert X(t)\rvert^2$ 就被称为功率 (Power)。即 $S_X(\omega)$ 的积分是功率，自然它也就是功率谱。

此外，功率谱 $S_X(\omega)$ 还是一个偶函数，即 $S_X(\omega)=S_X(-\omega)$：

\[\begin{equation} \begin{aligned} S_X(\omega) &=\int_{-\infty}^{\infty}R_X(\tau)\exp(-j\omega \tau)\mathrm{d}\tau\\ &=\int_{-\infty}^{\infty}R_X(\tau)\cos(\omega \tau)\mathrm{d}\tau- \underbrace{\int_{-\infty}^{\infty}R_X(\tau)\sin(\omega \tau)\mathrm{d}\tau}_{=0(奇函数)}\\ &=\int_{-\infty}^{\infty}R_X(\tau)\cos(\omega \tau)\mathrm{d}\tau\\ S_X(-\omega) &=\int_{-\infty}^{\infty}R_X(\tau)\cos(\omega \tau)\mathrm{d}\tau+ \underbrace{\int_{-\infty}^{\infty}R_X(\tau)\sin(\omega \tau)\mathrm{d}\tau}_{=0}\\ &=\int_{-\infty}^{\infty}R_X(\tau)\cos(\omega \tau)\mathrm{d}\tau\\ \end{aligned} \end{equation}\]

3.2.3. 线性系统对功率谱的影响

我们已经知道，当一个信号 $X(t)$ 通过一个线性系统时得到输出 $Y(t)$：

\[\begin{equation} Y(t)=\int_{-\infty}^{\infty}h(t-s)X(s)\mathrm{d}s \label{eq:linear-system} \end{equation}\]

其频谱会乘以线性系统的传递函数 $H(\omega)$：

\[\begin{equation} Y(\omega)=H(\omega)X(\omega) \end{equation}\]

在功率谱中，又会是什么样子呢？

根据公式 \eqref{eq:linear-system}，我们计算输出信号 $Y(t)$ 的相关函数：

\[\begin{equation} \begin{aligned} R_Y(t,s) &=\mathbb{E}[Y(t)Y(s)]\\ &=\mathbb{E} \left( \int_{-\infty}^{\infty}h(t-\tau)X(\tau)\mathrm{d}\tau \right) \left( \int_{-\infty}^{\infty}h(s-r)X(r)\mathrm{d}r \right)\\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h(t-\tau)h(s-r) \mathbb{E}[X(\tau)X(r)] \mathrm{d}\tau\mathrm{d}r\\ &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h(t-\tau)h(s-r) R_X(\tau-r) \mathrm{d}\tau\mathrm{d}r\\ \end{aligned} \end{equation}\]

上面的形式很像线性系统 $h$ 和相关函数 $R_X$ 的二维卷积，但实际上并不是（因为积分变量没法消掉）。

Note：判断一个积分是卷积，就看积分中几个函数自变量的取值加起来，能否刚好把积分变量抵消掉，且这个和就是卷积的点。

为此，我们令 $\widetilde{h}(t)=h(-t)$，则：

\[\begin{equation} \begin{aligned} R_Y(t,s) &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h(t-\tau)\widetilde{h}(r-s) R_X(\tau-r) \mathrm{d}\tau\mathrm{d}r\\ &=(h\circledast\widetilde{h}\circledast R_X)(t-s) \end{aligned} \end{equation}\]

至此，我们可以得出结论：线性系统不会改变随机信号的宽平稳性。

由于相关函数可以写成卷积的形式，其功率谱（相当于做傅里叶变换）就非常好计算了，就是卷积函数傅里叶变换的乘积：

\[\begin{equation} \begin{aligned} S_Y(\omega) &=H(\omega)\widetilde{H}(\omega)S_X(\omega)\\ \end{aligned} \end{equation}\]

其中，

\[\begin{equation} \begin{aligned} \widetilde{H}(\omega) &=\int_{-\infty}^{\infty}\widetilde{h}(t)\exp(-j\omega t)\mathrm{d}t\\ &=\int_{-\infty}^{\infty}h(-t)\exp(-j\omega t)\mathrm{d}t\\ &\overset{s=-t}{=}\overline{\int_{-\infty}^{\infty}h(s)\exp(-j\omega s)\mathrm{d}s}\\ &=\overline{H(w)} \end{aligned} \end{equation}\]

代入上式得：

\[\begin{equation} \begin{aligned} S_Y(\omega) &=H(\omega)\overline{H(\omega)}S_X(\omega)\\ &=\left\lvert H(\omega)\right\rvert^2S_X(\omega)\\ \end{aligned} \end{equation}\]

综上所述，当一个宽平稳的随机信号通过一个线性时不变 (LTI) 系统时：

输出仍然是宽平稳的随机信号
输出功率谱密度等于输入功率谱密度乘以系统传递函数的模的平方

Appendix

Apd.1. Proof of Bochner’s Theorem

下面我们证明Bochner定理，即一个函数 $f(x)$ 是正定的，当且仅当它的傅里叶变换非负：

\[\begin{equation} \int_{-\infty}^{\infty}f(x)\exp(-j\omega x)\mathrm{d}x\ge 0 \end{equation}\]

充分性

我们定义傅里叶变换：

\[\begin{equation} \mathcal{F}(\omega)=\int_{-\infty}^{\infty}f(x)\exp(-j\omega x)\mathrm{d}x \end{equation}\]

同样地，我们就有傅里叶反变换：

\[\begin{equation} f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathcal{F}(\omega)\exp(j\omega x)\mathrm{d}\omega \label{eq:inv_fourier} \end{equation}\]

当 $\mathcal{F}(\omega)\ge 0$ 时，我们希望证明 $f(x)$ 是正定的。

我们先证明复指数 $\exp(j\omega x)$ 是正定的。$\forall n,\forall x_1,\dots,x_n$，我们构建矩阵：

\[\begin{equation} R_{ij}=\exp(j\omega (x_i-x_j)) \end{equation}\]

$\forall z=(z_1,\dots,z_n)^T\in\mathbb{C}^n$，我们有：

\[\begin{equation} \begin{aligned} z^HRz &=\sum_{i=1}^n\sum_{j=1}^n R_{ij}z_i\overline{z_j}\\ &=\sum_{i=1}^n\sum_{j=1}^n \exp(j\omega (x_i-x_j))z_i\overline{z_j}\\ &=\left(\sum_{i=1}^n \exp(j\omega x_i)z_i\right)\left(\sum_{j=1}^n \exp(-j\omega x_j)\overline{z_j}\right)\\ &=\left(\sum_{i=1}^n \exp(j\omega x_i)z_i\right)\left(\overline{\sum_{j=1}^n \exp(j\omega x_j)z_j}\right)\\ &=\left\lvert \sum_{i=1}^n \exp(j\omega x_i)z_i\right\rvert^2\\ &\ge 0\\ \end{aligned} \end{equation}\]

因此复指数 $\exp(j\omega x)$ 是正定的。

又由于正定函数用正系数做线性组合，得到的函数仍然是正定的，即 $\forall f_1,\dots,f_n\ge 0$，$\sum_{i=1}^n f_i\exp(j\omega x)$ 是正定的。

将上式连续化就可以得到：

\[\begin{equation} f(x)=\int_{-\infty}^{\infty}\underbrace{\frac{1}{2\pi}\mathcal{F}(\omega)}_{\ge 0}\exp(j\omega x)\mathrm{d}\omega \end{equation}\]

一定是正定的，充分性得证。

必要性

给定 $n$，$\forall x_1,\dots,x_n$，我们取 $z=\left(\exp(-j\omega x_1),\dots,\exp(-j\omega x_n)\right)^T$，令矩阵 $R_{ij}=f(x_i-x_j)$。

由于 $f(x)$ 是正定的，我们有：

\[\begin{equation} \begin{aligned} z^HRz &=\sum_{i=1}^n\sum_{j=1}^n f(x_i-x_j)\exp(-j\omega x_i)\overline{\exp(-j\omega x_j)}\\ &=\sum_{i=1}^n\sum_{j=1}^n f(x_i-x_j)\exp(-j\omega (x_i-x_j))\\ &\ge 0\\ \end{aligned} \end{equation}\]

下面我们对上式的求和进行连续化。由于求和连续化之后应当变为有限区间上的积分，然后再对积分上下限取极限才能得到傅里叶变换中的无穷积分形式，因此我们这里的连续化也是遵循这两步。

\[\begin{equation} \begin{aligned} \frac{1}{T}z^HRz &=\frac{1}{T}\sum_{i=1}^n\sum_{j=1}^n f(x_i-x_j)\exp(-j\omega (x_i-x_j))\\ &\to \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t-s)\exp(-j\omega (t-s))\mathrm{d}t\mathrm{d}s\\ &\ge 0 \end{aligned} \end{equation}\]

注意这里多乘了一个常数 $\frac{1}{T}$，是为了后续的推导更加方便，且乘这个常数并不会改变结论的成立。

我们令 $u=t-s,v=t+s$，换元得：

\[\begin{equation} \begin{aligned} \text{原式} &=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t-s)\exp(-j\omega (t-s))\mathrm{d}t\mathrm{d}s\\ &=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(u)\exp(-j\omega u)\mathrm{d}t\mathrm{d}s\\ \label{eq:variable-change} \end{aligned} \end{equation}\]

其中，

\[\begin{equation} \begin{aligned} \mathrm{d}t\mathrm{d}s &=\left\lvert \det\left(\frac{\partial(t,s)}{\partial (u,v)}\right) \right\rvert\mathrm{d}u\mathrm{d}v\\ &= \frac{1}{\left\lvert\det\left(\frac{\partial(u,v)}{\partial (t,s)}\right)\right\rvert} \mathrm{d}u\mathrm{d}v\\ &= \frac{1}{\left\lvert\det \begin{pmatrix} 1 & -1\\ 1 & 1\\ \end{pmatrix}\right\rvert} \mathrm{d}u\mathrm{d}v\\ &=\frac{1}{2}\mathrm{d}u\mathrm{d}v \end{aligned} \end{equation}\]

因此，

\[\begin{equation} \begin{aligned} \text{原式} &=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(u)\exp(-j\omega u)\mathrm{d}t\mathrm{d}s\\ &=\frac{1}{2T}\underset{\Omega}{\int\int} f(u)\exp(-j\omega u)\mathrm{d}u\mathrm{d}v\\ \end{aligned} \end{equation}\]

这里的积分区域 $\Omega$ 是下面的菱形：

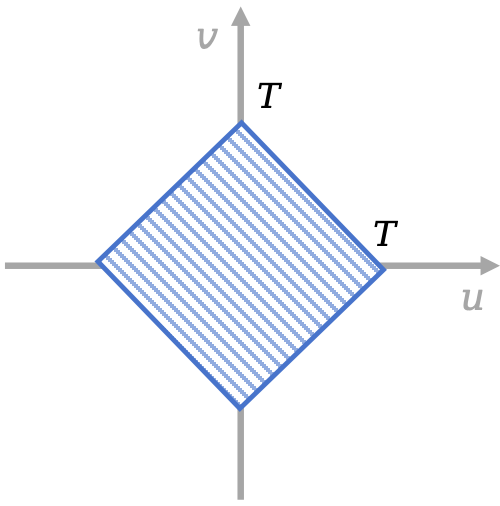
Bochner

我们先对 $v$ 积分得：

\[\begin{equation} \begin{aligned} \text{原式} &=\frac{1}{2T}\underset{\Omega}{\int\int} f(u)\exp(-j\omega u)\mathrm{d}u\mathrm{d}v\\ &=\frac{1}{2T}\left( \int_{-T}^0f(u)\exp(-j\omega u)\mathrm{d}u\int_{-u-T}^{u+T}\mathrm{d}v + \int_{0}^Tf(u)\exp(-j\omega u)\mathrm{d}u\int_{u-T}^{-u+T}\mathrm{d}v \right)\\ &=\frac{1}{2T}\left( \int_{-T}^0f(u)\exp(-j\omega u)2(u+T)\mathrm{d}u - \int_{0}^Tf(u)\exp(-j\omega u)2(u-T)\mathrm{d}u\ \right)\\ &=\frac{1}{T}\int_{-T}^T(T-\lvert u\rvert)f(u)\exp(-j\omega u)\mathrm{d}u\\ &=\int_{-T}^T(1-\frac{\lvert u\rvert}{T})f(u)\exp(-j\omega u)\mathrm{d}u\\ &\ge 0 \end{aligned} \end{equation}\]

我们令积分上下限 $T\to\infty$，则有：

\[\begin{equation} \begin{aligned} \lim_{T\to\infty}\int_{-T}^T(1-\frac{\lvert u\rvert}{T})f(u)\exp(-j\omega u)\mathrm{d}u &=\int_{-\infty}^{\infty}f(u)\exp(-j\omega u)\mathrm{d}u\\ &=\mathcal{F}(\omega)\\ &\ge 0 \end{aligned} \end{equation}\]

必要性得证。

至此，整个Bochner定理的证明完毕。

宽平稳随机过程相关函数的时频分析