随机过程(4)

在之前的内容中，我们主要研究了两个随机变量之间的相关。相关代表了这两个随机变量之间的某种线性关联，它给出了两个随机变量之间线性关联的强弱，也就是说一个随机变量在多大程度上能够用另一个随机变量线性表出。

在这一篇文章中，我们将对相关的概念进行一定程度的扩充，研究多个随机变量之间的相关 (multivariate correlation)，我们希望了解其联合分布 (joint distribution) 的统计性质。

多元联合分布只有在极少数情况下（比如说多元高斯）才会有比较好的答案。在一般情况下，我们很难获得其多元联合分布的一些信息。

这样一来，我们就需要一些数学工具，在不知道联合分布的前提下，仍然让我们能够对多个随机变量之间的相关进行研究。这个工具就是相关矩阵 (correlation matrix)：

考虑 $X=(X_1,X_2,\ldots,X_n)^T$ 这 $n$ 个随机变量，其相关矩阵定义为：

\[\begin{equation} R_X=\mathbb{E}\left[XX^T\right] \end{equation}\]

其中，矩阵的第 $(i,j)$ 个元素就是 $X_i$ 和 $X_j$ 的相关：

\[\begin{equation} R_{ij}=\mathbb{E}\left[X_iX_j\right] \end{equation}\]

显然，相关矩阵是一个对称矩阵，因为 $R_{ij}=R_{ji}$。

下面，我们分别在四个场景中研究多个随机变量之间的相关。

一、去相关

去相关 (decorrelation) 也称为白化 (whitening)，它的作用是将多个随机变量之间的相关去掉，使得它们之间的相关为零。

也就是说，我们希望找到一个矩阵 $A\in\mathbb{R}^{n\times n}$，使得 $Y=AX\in\mathbb{R}^n$ 满足：

\[\begin{equation} \forall i\ne j,\mathbb{E}[Y_iY_j]=0 \end{equation}\]

即 $R_Y$ 是一个对角矩阵。

这个任务看起来不太容易完成，因为我们需要用 $\binom{n}{2}=\frac{n(n-1)}{2}$ 个条件来求解 $A$ 中的 $n^2$ 个元素。但我们把这 $\binom{n}{2}$ 个相关都组织成为一个矩阵的形式，使得这个问题就有路可循。

事实上，我们可以写出 $R_Y$ 的形式：

\[\begin{equation} \begin{aligned} R_Y &=\mathbb{E}\left[ YY^T \right]\\ &=\mathbb{E}\left[AXX^TA^T\right]\\ &=A\mathbb{E}\left[XX^T\right]A^T\\ &=AR_XA^T \end{aligned} \end{equation}\]

由于 $R_X$ 是一个对称矩阵，因此我们一定可以对其进行特征值分解：

\[\begin{equation} \begin{aligned} R_X &=\sum_{k=1}^{n}\lambda_kU_kU_k^T\\ &=U\Lambda U^T \end{aligned} \end{equation}\]

其中，$U$ 是一个正交矩阵，$\Lambda=\text{diag}(\lambda_1,\lambda_2,\ldots,\lambda_n)$ 是一个对角矩阵，其对角元素就是 $R_X$ 的特征值。此外，我们已知 $R_X\ge 0$，即它是一个半正定矩阵，因此我们有 $\lambda_k\ge 0$。

因此，我们只要取 $A=U^T$，就可以将 $R_Y$ 变成一个对角矩阵：

\[\begin{equation} \begin{aligned} R_Y &=AR_XA^T\\ &=U^TU\Lambda U^TU\\ &=\Lambda \end{aligned} \end{equation}\]

二、Karhunen-Loève 展开

2.1. 离散时间的 K-L 展开

我们继续上面的讨论。

由于 $Y=AX$，因此 $X$ 可以写为：

\[\begin{equation} \begin{aligned} X&=A^{-1}Y\\ &=U^TY\\ &=\sum_{k=1}^{n}U_k^TY_k\\ \end{aligned} \end{equation}\]

这里我们对 $X$ 进行了一个展开 (expansion)，这个展开具有如下的特点。

我们可以发现：

不同的特征向量之间是正交的，即 $U_i^TU_j=0(i\ne j)$。
$Y$ 的不同分量之间是相互独立（即正交）的，即 $\mathbb{E}[Y_iY_j]=0(i\ne j)$。

也就是说，我们在一组正交基 $U=\lbrace U_1,U_2,\dots,U_n\rbrace$ 下，把 $X$ 进行了展开，且展开的系数 $Y=\lbrace Y_1,Y_2,\dots,Y_n\rbrace$ 也是两两正交的。同时，所有的随机性都集中在展开系数中，正交基底并没有任何的随机性。因此，这种展开是一种【双正交】的展开 (Biorthogonal Expansion)。

在随机过程的领域，上述的展开就是鼎鼎大名的 Karhunen-Loève (K-L) 展开。

下面，我们将K-L展开推广到连续时间的情况。在这里，我们可以看到对随机过程进行谱分析的另一种方法。

2.2. 连续时间的 K-L 展开 (Mercer 定理)

考虑连续时间的随机过程 $X(t)$，对照上面的 $X=(X_1,X_2,\ldots,X_n)^T$。

我们希望把随机过程 $X(t)$ 进行展开，把其中的随机性和过程性解耦。其中：

过程性：留下与上面的基底向量 $U$ 对应的基底函数，这些函数都是与 $t$ 相关的，且没有随机性。
随机性：留下与系数 $Y$ 相关的随机变量，这些随机变量与 $t$ 无关，只与随机性相关。

也就是说，我们希望做到下面的展开：

\[\begin{equation} X(t)=\sum_{k=-\infty}^{+\infty}\alpha_k\phi_k(t) \end{equation}\]

这个和傅里叶展开的形式比较类似。在傅里叶展开中，我们选择的基底函数为复指数函数：$\phi_k(t)=\exp(-j\omega_k t)$。但在这里，我们希望我们的展开能够保留双正交性质。在傅里叶展开中，我们只能保证基底函数是正交的，但没法保证系数的正交性。

我们的求解思路如下：先假设 $\phi_k$ 已经是正交的，求出 $\alpha_k$ 之后，再验证 $\phi_k$ 是否正交。

我们在某一个区间 $I$ 上对 $X(t)$ 进行展开。假设 $\lbrace\phi_k\rbrace$ 是一组标准正交基，即：

\[\begin{equation} \begin{aligned} \int_I\phi_i(t)\phi_j(t)\mathrm{d}t&=0,(\forall i\ne j)\\ \int_I\phi_k^2(t)\mathrm{d}t&=1 \end{aligned} \end{equation}\]

此时，我们能简单地写出 $\alpha_k$ 的形式：

\[\begin{equation} \alpha_k=\int_IX(t)\phi_k(t)\mathrm{d}t \label{eq:alpha} \end{equation}\]

由于 $\alpha_k$ 也具有正交性，即 $\forall i\ne j$，都有：

\[\begin{equation} \begin{aligned} \mathbb{E}[\alpha_i\alpha_j] &=\mathbb{E}\left[ \int_IX(t)\phi_i(t)\mathrm{d}t \int_IX(s)\phi_j(s)\mathrm{d}s \right]\\ &= \int_I\int_I \mathbb{E}[X(t)X(s)] \phi_i(t)\phi_j(s) \mathrm{d}t\mathrm{d}s\\ &= \int_I\int_I R_X(t,s) \phi_i(t)\phi_j(s) \mathrm{d}t\mathrm{d}s\\ &=0 \end{aligned} \end{equation}\]

也就是说，我们希望找到一组标准正交的基底函数 $\lbrace\phi_k\rbrace$，满足上面的条件。

这个积分比较复杂，但我们可以通过矩阵和向量的形式来看待，从而对结果获得比较好的一些认知。

具体来说，我们对上式做三件事情：

把积分变为求和
把二元函数 $R_X(t,s)$ 变为矩阵 $R_X$ 的某一个元素 $R_X(m,n)$
把一元函数 $\phi_i(t)$ 变为向量 $\phi_i$ 的某一个元素 $\phi_i(m)$

如果有了这样的转换，我们就可以把上式写为：

\[\begin{equation} \begin{aligned} \mathbb{E}[\alpha_i\alpha_j] &\Rightarrow \sum_{m=1}^n\sum_{n=1}^n R_X(m,n)\phi_i(m)\phi_j(n)\\ &=\phi_i^TR_X\phi_j\\ &=0 \end{aligned} \end{equation}\]

此时，$\phi_i$ 和 $\phi_j$ 都是 $R_X$ 的特征向量，因为：

\[\begin{equation} \begin{aligned} \phi_i^TR_X\phi_j &=\phi_i^T\lambda_j\phi_j\\ &=\lambda_j\cdot\phi_i^T\phi_j\\ &=0 \end{aligned} \end{equation}\]

回到连续时间的版本，有了上面的认知，我们可以发现我们所寻找的 $\phi_i$ 一定要满足：

\[\begin{equation} \int_IR_X(t,s)\phi_i(s)\mathrm{d}s=\lambda_i\phi_i(t) \label{eq:eigenfunction} \end{equation}\]

即我们想要系数 $\alpha_k$ 相互正交，我们只需要取基底函数 $\phi_k$ 为相关函数 $R_X(t,s)$ 的特征函数（也称为本征函数, eigenfunction）即可。

我们验证一下公式 \eqref{eq:eigenfunction} 的解是否满足正交性。如果不满足，我们前面所做的所有工作都是白费的。

幸运的是，答案是肯定的。这是因为，相关函数 $R_X(t,s)$ 是对称的。对称函数的本征解一定是正交的，就像对称矩阵的特征向量一定是正交的一样。

总结一下连续时间的Karhunen-Loève展开的步骤：

求解本征方程 \eqref{eq:eigenfunction}，得到基底函数 $\phi_k$。
利用公式 \eqref{eq:alpha}，计算出系数 $\alpha_k$。

我们可以保证，这样解出来的系数和基底函数都是正交的，整个展开具有双正交性质。

上面的定理一般称为 Mercer 定理，它可以把任意一个连续时间的随机过程进行双正交展开。

2.3. 宽平稳条件下的解形式

在一般情况下，公式 \eqref{eq:eigenfunction} 中对应的本征解比较复杂，很难有初等解。但是当我们对 $R_X(t,s)$ 进行一些假设时，我们就能写出比较好的解形式。

具体来说，假设 $X(t)$ 是一个宽平稳的随机过程，我们在 $I=[-\frac{T}{2},\frac{T}{2}]$ 上对 $X(t)$ 进行展开。

我们需要解下面的积分方程：

\[\begin{equation} \int_{-\frac{T}{2}}^{\frac{T}{2}} R_X(t-s)\phi_k(s) \mathrm{d}s =\lambda_k\phi_k(t) \end{equation}\]

上面方程的解正好就是复指数函数：

\[\begin{equation} \phi_k(t)=\exp\left(j\frac{2k\pi}{T}t\right) \end{equation}\]

我们来验证这个解：

\[\begin{equation} \begin{aligned} \text{LHS} &= \int_{-\frac{T}{2}}^{\frac{T}{2}} R_X(\underbrace{t-s}_{=s'}) \exp\left(j\frac{2k\pi}{T}s\right) \mathrm{d}s\\ &= \int_{t-\frac{T}{2}}^{t+\frac{T}{2}} R_X(s') \exp\left(j\frac{2k\pi}{T}(t-s')\right) \mathrm{d}s'\\ &= \left(\int_{t-\frac{T}{2}}^{t+\frac{T}{2}} R_X(s') \exp\left(-j\frac{2k\pi}{T}s'\right) \mathrm{d}s'\right) \cdot \underbrace{\exp\left(j\frac{2k\pi}{T}t\right)}_{\phi_k(t)} \end{aligned} \end{equation}\]

因此，我们希望前面的系数是一个常数。但现在积分限中包含了 $t$，我们希望把 $t$ 消掉。这很自然的能够联想到利用周期性。如果被积函数是一个周期为 $T$ 的周期函数，那么我们就可以把积分限中的积分起点 $t$ 消掉。

显然，复指数 $\exp\left(j\frac{2k\pi}{T}t\right)$ 是一个周期为 $T$ 的周期函数。但相关函数的周期性却没办法保证。

此时，我们再增加一些假设。假设相关函数也是一个以 $T$ 为周期的周期函数，即 $R_X(\tau)=R_X(\tau+T)$。此时：

\[\begin{equation} \begin{aligned} \text{LHS} &= \left(\int_{\frac{T}{2}}^{\frac{T}{2}} R_X(s') \exp\left(-j\frac{2k\pi}{T}s'\right) \mathrm{d}s'\right) \cdot \phi_k(t)\\ &=\lambda_k\phi_k(t)\\ &=\text{RHS} \end{aligned} \end{equation}\]

综上所述，对于一个宽平稳的随机过程 $X(t)$，如果它的相关函数是一个周期函数 $R_X(\tau)=R_X(\tau+T)$，那么它的【傅里叶展开】（注意不是 Karhunen-Loève 展开）：

\[\begin{equation} X(t)=\sum_{k=-\infty}^{\infty}\alpha_k\exp\left(j\frac{2k\pi}{T}t\right) \end{equation}\]

就满足双正交性质。

三、宽平稳随机过程的谱分析：Stieltjes 积分

我们接着上面的内容继续深入讨论。

上面我们已经知道，对于具有周期相关函数的宽平稳过程，其傅里叶展开满足双正交性质。这里引入了一个新的假设，即相关函数 $R_X(t,s)$ 是一个周期函数 $R_X(\tau)=R_X(\tau+T)$。

这个假设能否消除呢？回顾上一篇的内容，一个自然的想法就是令 $T\to\infty$，这样相关函数就变成了一个非周期函数。如果这件事情可以做到，我们就能对任何一个随机过程本身进行谱分析。

然而正如我们之前所说的，令 $T\to\infty$ 可能会使得 $\alpha_k$ 的积分发散。为了解决这个问题，前面我们是通过 Wiener-Khintchine 定理，通过对相关函数而不是随机过程进行谱分析，来解决这个问题的。

但是现在不同了，我们有了双正交这个深刻的认知，我们已经知道了 $\alpha_k$ 在期望的意义下是两两正交的，即：

\[\begin{equation} \mathbb{E}[\alpha_i\alpha_j]=0\quad\forall i\neq j \end{equation}\]

此时，我们就有了处理这个问题的另一种方法：利用 Stieltjes 积分。

我们熟知的积分是指黎曼积分 (Riemann integral)，它的定义是：

\[\begin{equation} \int_a^b f(x)\mathrm{d}x:=\lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta x_k \end{equation}\]

而 Stieltjes 积分的积分变量则是另一个函数：

\[\begin{equation} \int_a^b f(x)\mathrm{d}g(x):=\lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta g(x_k) \end{equation}\]

其中，$\Delta g(x_k)=g(x_k)-g(x_{k-1})$。

回到我们的问题中。我们希望把 $X(t)$ 写成下面的傅里叶级数的形式：

\[\begin{equation} X(t)\overset{?}{=}\int_{-\infty}^{\infty}\alpha(\omega)\exp(j\omega t)\mathrm{d}\omega \end{equation}\]

但由于 $\alpha(\omega)$ 在某些频率上发散，因此我们做不到这样的事情。但是我们可以把这些发散的点都写到积分变量中，只要我们不对其进行微分，就不会有问题：

\[\begin{equation} X(t)=\int_{-\infty}^{\infty}\exp(j\omega t)\mathrm{d}F_X(\omega) \label{eq:sepc-rep} \end{equation}\]

这里的 $F_X$ 称为谱函数。可以发现，$\mathrm{d}F_X(\omega)$ 就相当于傅里叶分解中的系数 $\alpha(\omega)$。

上面的公式 \eqref{eq:sepc-rep} 非常重要，它称为一个随机过程的谱表示 (spectral representation)。

3.1. 谱表示中的双正交性质

谱表示的双正交体现在：

\[\begin{equation} \mathbb{E}\left[ \mathrm{d}F_X(\omega_1)\overline{\mathrm{d}F_X(\omega_2)} \right]= \begin{cases} 0,&\omega_1\ne\omega_2\\ \frac{1}{2\pi}S_X(\omega)\mathrm{d}\omega,&\omega_1=\omega_2=\omega \end{cases} \end{equation}\]

其中，$S_X(\omega)$ 是 $X(t)$ 的功率谱密度。

下面我们来证明 $\omega_1=\omega_2=\omega$ 时的结论。

考虑 $X(t)$ 的相关函数。注意 $X(t)$ 这里出现了复数，因此是复相关：

\[\begin{equation} \begin{aligned} R_X(t,s) &=R_X(t-s)\\ &=\mathbb{E}\left[X(t)\overline{X(s)}\right]\\ &=\mathbb{E}\left[ \int_{-\infty}^{\infty}\exp(j\omega_1 t)\mathrm{d}F_X(\omega_1) \overline{\int_{-\infty}^{\infty}\exp(j\omega_2 s)\mathrm{d}F_X(\omega_2)} \right]\\ &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} \exp(j(\omega_1 t-\omega_2 s)) \mathbb{E}\left[ \mathrm{d}F_X(\omega_1) \overline{\mathrm{d}F_X(\omega_2)} \right] \end{aligned} \end{equation}\]

注意到这个积分在 $\omega_1\ne\omega_2$ 时一律为0，因此这个两重积分实际上只有一重，即在 $\omega_1=\omega_2=\omega$ 时才不为0。

因此：

\[\begin{equation} R_X(t,s)= \int_{-\infty}^{\infty} \exp(j\omega (t-s)) \mathbb{E}\left[\left\lvert \mathrm{d}F_X(\omega) \right\rvert^2\right] \end{equation}\]

同时，Wiener-Khintchine 定理告诉我们，相关函数可以写成功率谱密度的傅里叶反变换：

\[\begin{equation} R_X(t,s)= \frac{1}{2\pi}\int_{-\infty}^{\infty} S_X(\omega)\exp(j\omega(t-s))\mathrm{d}\omega \end{equation}\]

比较上下两个等式得：

\[\begin{equation} \mathbb{E}\left[\left\lvert \mathrm{d}F_X(\omega) \right\rvert^2\right]=\frac{1}{2\pi}S_X(\omega)\mathrm{d}\omega \label{eq:spec-pow} \end{equation}\]

这就是谱函数和功率谱密度之间的联系。

3.2. 重新看待线性系统对功率谱的影响

在前面的内容中，我们通过比较复杂的数学运算，得出了线性系统对宽平稳随机过程功率谱的影响

具体来说，当一个宽平稳的随机信号通过一个线性时不变系统时：

\[\begin{equation} Y(t)=\int_{-\infty}^{\infty}h(t-\tau)X(\tau)\mathrm{d}\tau \end{equation}\]

我们有一下两个结论：

输出信号 $Y(t)$ 仍然是宽平稳的随机信号
输出功率谱密度等于输入功率谱密度乘以系统传递函数的模的平方：

\[\begin{equation} S_Y(\omega)=\left\lvert H(\omega)\right\rvert^2S_X(\omega)\\ \end{equation}\]

现在，我们利用双正交性，来重新证明这个结论。

考虑 $X(\tau)$ 的谱表示：

\[\begin{equation} X(\tau)=\int_{-\infty}^{\infty}\exp(j\omega \tau)\mathrm{d}F_X(\omega) \end{equation}\]

代入线性系统中，得：

\[\begin{equation} \begin{aligned} Y(t) &=\int_{-\infty}^{\infty}h(t-\tau)X(\tau)\mathrm{d}\tau\\ &= \int_{-\infty}^{\infty} h(t-\tau) \left(\int_{-\infty}^{\infty} \exp(j\omega \tau) \mathrm{d}F_X(\omega)\right) \mathrm{d}\tau\\ &= \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} h(\underbrace{t-\tau}_{=\tau'}) \exp(j\omega \tau) \mathrm{d}\tau \right) \mathrm{d}F_X(\omega)\\ &= \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} h(\tau') \exp(j\omega (t-\tau')) \mathrm{d}\tau' \right) \mathrm{d}F_X(\omega)\\ &= \int_{-\infty}^{\infty} \underbrace{\left( \int_{-\infty}^{\infty} h(\tau') \exp(-j\omega \tau') \mathrm{d}\tau' \right)}_{=H(\omega)} \exp(j\omega t) \mathrm{d}F_X(\omega)\\ &= \int_{-\infty}^{\infty} H(\omega) \exp(j\omega t) \mathrm{d}F_X(\omega)\\ \end{aligned} \end{equation}\]

同时，由于 $Y(t)$ 也是宽平稳的，因此它也有谱表示：

\[\begin{equation} Y(t)=\int_{-\infty}^{\infty}\exp(j\omega t)\mathrm{d}F_Y(\omega) \end{equation}\]

对应上下两式，得到：

\[\begin{equation} \mathrm{d}F_Y(\omega)=H(\omega)\mathrm{d}F_X(\omega) \end{equation}\]

同时，根据谱函数和功率谱的关系 \eqref{eq:spec-pow}，我们有：

\[\begin{equation} \begin{aligned} \frac{1}{2\pi}S_Y(\omega)\mathrm{d}\omega &=\mathbb{E}\left[\left\lvert \mathrm{d}F_Y(\omega) \right\rvert^2\right]\\ &=\left\lvert H(\omega) \right\rvert^2 \cdot \mathbb{E}\left[\left\lvert \mathrm{d}F_X(\omega) \right\rvert^2\right]\\ &=\left\lvert H(\omega) \right\rvert^2 \cdot \frac{1}{2\pi}S_X(\omega)\mathrm{d}\omega\\ &=\frac{1}{2\pi}\left\lvert H(\omega) \right\rvert^2S_X(\omega)\mathrm{d}\omega \end{aligned} \end{equation}\]

因此，

\[\begin{equation} S_Y(\omega)=\left\lvert H(\omega) \right\rvert^2 S_X(\omega) \end{equation}\]

得证。

3.3. 宽平稳随机过程的进一步认识

在有了双正交这个性质之后，我们可以对宽平稳随机过程进行更深刻的认识。

我们指出，宽平稳的随机过程 $X(t)$ 和复指数 $\exp(j\omega t)$ 是有着对应关系的。下面我们从理论上证明这一点。

为了把二者对应起来，我们假设 $X(t)$ 是处于某一个由随机过程构成的线性空间空间 $H_1$ 中，而 $\exp(j\omega t)$ 是处于另一个由复函数构成的线性空间空间 $H_2$ 中。

我们希望说明：$X(t)$ 和 $\exp(j\omega t)$ 构成了这两个空间的一个【等距同构】(isometry)：

\[\begin{equation} \left\lVert X(t)-X(s)\right\rVert_{H_1}^2 = \left\lVert \exp(j\omega t)-\exp(j\omega s)\right\rVert_{H_2}^2 \end{equation}\]

下面我们需要适当地选取两个空间中的距离度量 $\lVert\cdot\rVert_{H_1}$ 和 $\lVert\cdot\rVert_{H_2}$，使得上式成立。

对于 $H_1$ 空间，我们采用均方距离：

\[\begin{equation} \left\lVert X(t)-X(s)\right\rVert_{H_1}^2=\mathbb{E}\left\lvert X(t)-X(s)\right\rvert^2 \end{equation}\]

对于 $H_2$ 空间，我们采用 $X(t)$ 的功率谱来定义距离：

\[\begin{equation} \left\lVert \exp(j\omega t)-\exp(j\omega s)\right\rVert_{H_2}^2 =\frac{1}{2\pi} \int_{-\infty}^{\infty} S_X(\omega) \left\lvert \exp(j\omega t)-\exp(j\omega s) \right\rvert^2 \mathrm{d}\omega \end{equation}\]

这二者的相等是不难看出的。事实上，对于等式左侧：

\[\begin{equation} \begin{aligned} \text{LHS} &=\left\lVert X(t)-X(s)\right\rVert_{H_1}^2\\ &=\mathbb{E}\left\lvert X(t)-X(s)\right\rvert^2\\ &=\mathbb{E}\left\lvert X(t)\right\rvert^2+ \mathbb{E}\left\lvert X(s)\right\rvert^2- \mathbb{E}\left\lvert X(t)\overline{X(s)}\right\rvert- \mathbb{E}\left\lvert \overline{X(t)}X(s)\right\rvert\\ &=2R_X(0)-R_X(t-s)-R_X(s-t) \end{aligned} \end{equation}\]

对于等式右侧：

\[\begin{equation} \begin{aligned} \text{RHS} &=\left\lVert \exp(j\omega t)-\exp(j\omega s)\right\rVert_{H_2}^2\\ &=\frac{1}{2\pi} \int_{-\infty}^{\infty} S_X(\omega) \left\lvert \exp(j\omega t)-\exp(j\omega s) \right\rvert^2 \mathrm{d}\omega\\ &=\frac{1}{2\pi} \int_{-\infty}^{\infty} S_X(\omega) \left( 2-\exp(j\omega (t-s))-\exp(j\omega (s-t)) \right) \mathrm{d}\omega\\ &=2\cdot\underbrace{\frac{1}{2\pi} \int_{-\infty}^{\infty} S_X(\omega) \mathrm{d}\omega}_{=R_X(0)} - \underbrace{\frac{1}{2\pi} \int_{-\infty}^{\infty} S_X(\omega) \exp(j\omega (t-s)) \mathrm{d}\omega}_{=R_X(t-s)}\\ &\qquad- \underbrace{\frac{1}{2\pi} \int_{-\infty}^{\infty} S_X(\omega) \exp(j\omega (s-t)) \mathrm{d}\omega}_{=R_X(s-t)} \\ &=2R_X(0)-R_X(t-s)-R_X(s-t) \end{aligned} \end{equation}\]

因此，二者是相等的。

Note：这里的形式和我们之前推导的不太一样。我们之前推导的均方距离为：
\[\begin{equation} \mathbb{E}\left\lvert X(t)-X(s)\right\rvert^2=2(R_X(0)-R_X(t-s)) \end{equation}\]
这是因为这里引入了复数，需要考虑共轭。但其实本质上是一样的。

四、主成分分析

主成分分析 (Principal Component Analysis, PCA) 是数学分析和机器学习中一个非常重要的操作。它的作用是将一个高维的分布投影到一个低维的空间中，同时保留分布中的主要信息。

也就是说，我们希望找到一个向量 $\alpha\in\mathbb{R}^n$，当我们把 $X$ 投影到 $\alpha$ 上时，得到的新的随机变量 $\text{Proj}_{\alpha}(X)$ 具有最大的方差：

\[\begin{equation} \max_{\alpha\in\mathbb{R}^n}\mathbb{E}\left\lVert \text{Proj}_{\alpha}(X)\right\rVert^2 \end{equation}\]

事实上，我们可以证明：

\[\begin{equation} \begin{aligned} \mathbb{E}\left\lVert \text{Proj}_{\alpha}(X)\right\rVert^2 &=\mathbb{E}\left\lVert \frac{\alpha^TX}{\alpha^T\alpha}\cdot\alpha \right\rVert^2\\ &= \frac{\mathbb{E}\left\lvert \alpha^TX\right\rvert^2}{\lVert\alpha\rVert^4}\cdot\lVert\alpha\rVert^2\\ &=\frac{\mathbb{E}\left\lvert \alpha^TX\right\rvert^2}{\lVert\alpha\rVert^2}\\ &=\mathbb{E}\left( \frac{\alpha^T}{\lVert \alpha\rVert}\cdot X \right)^2 \end{aligned} \end{equation}\]

因此，当我们希望最大化方差时：

\[\begin{equation} \begin{aligned} &\max_{\alpha\in\mathbb{R}^n}\mathbb{E}\left\lVert \text{Proj}_{\alpha}(X)\right\rVert^2 =\max_{\alpha\in\mathbb{R}^n}\mathbb{E}\left( \frac{\alpha^T}{\lVert \alpha\rVert}\cdot X \right)^2\\ &\iff \max_{\alpha\in\mathbb{R}^n}\mathbb{E}\left( \alpha^TX \right)^2\quad\text{s.t.} \lVert\alpha\rVert^2=1 \end{aligned} \end{equation}\]

其中，

\[\begin{equation} \begin{aligned} \mathbb{E}\left(\alpha^TX\right)^2 &=\mathbb{E}\left(\alpha^TX\right)\left(X^T\alpha\right)\\ &=\alpha^T\mathbb{E}\left(XX^T\right)\alpha\\ &=\alpha^TR_X\alpha\\ \end{aligned} \end{equation}\]

因此，我们的优化问题就变成：

\[\begin{equation} \max_{\alpha}\alpha^TR_X\alpha\quad\text{s.t.} \lVert\alpha\rVert^2=1 \end{equation}\]

我们使用拉格朗日乘子法求解这个优化问题。考虑拉格朗日函数：

\[\begin{equation} L(\alpha,\lambda) =\alpha^TR_X\alpha-\lambda\left(\lVert\alpha\rVert^2-1\right) \end{equation}\]

对 $\alpha$ 求导：

\[\begin{equation} \nabla_{\alpha} L(\alpha,\lambda)=2R_X\alpha-2\lambda\alpha\\ \end{equation}\]

令上式为0解得 $\alpha$ 满足：

\[\begin{equation} R_X\alpha=\lambda\alpha \end{equation}\]

也就是说，$\alpha$ 是 $R_X$ 的一个特征向量，对应的特征值为 $\lambda$。更重要的是，由于我们要最大化方差，因此 $\lambda$ 就是 $R_X$ 的最大特征值。

综上所述，PCA所求的第一个投影向量 $\alpha$ 就是 $R_X$ 的最大特征值所对应的特征向量。

当我们希望在与 $\alpha$ 正交的方向上寻找第二个投影向量时，我们可以取 $\beta$ 为 $R_X$ 的次大特征值所对应的特征向量，以此类推。

FurtherMore

如下图所示，考虑两个随机变量 $X_1$ 和 $X_2$，其主成分向量为 $\alpha$。那么 $\alpha$ 与 $X_1$ 的夹角 $\theta$ 是否与 $X_1$ 和 $X_2$ 的相关性有关系呢？

PCA

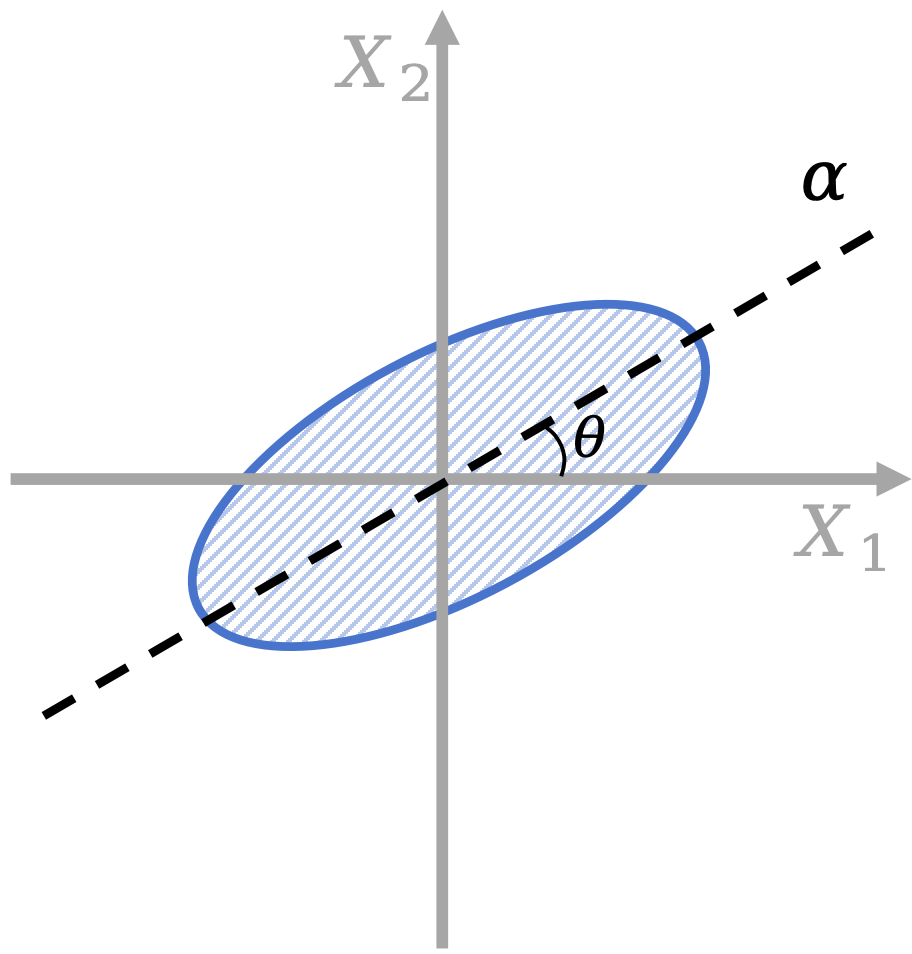
首先我们做一些假设。设两个随机变量的均值为0，方差为1，其相关为 $\rho=\mathbb{E}\left[X_1X_2\right]$。

令 $X=(X_1,X_2)^T$，则 $R_X$ 可以写为：

\[\begin{equation} R_X =\begin{bmatrix} 1&\rho\\ \rho&1 \end{bmatrix} \end{equation}\]

因此，$R_X$ 的两个特征值分别为 $\lambda_1=1+\rho$ 和 $\lambda_2=1-\rho$，且 $\lambda_1$ 对应的特征向量为 $\alpha=(1,1)^T$，$\lambda_2$ 对应的特征向量为 $\beta=(-1,1)^T$。

综上所述，$\alpha$ 与 $X_1$ 的夹角 $\theta$ 为始终为 $\frac{\pi}{4}$，与相关系数 $\rho$ 无关。

下面就引出了两个问题：

Q1: $\theta$ 和什么有关？

A1: $\theta$ 只和二者的方差有关。由于我们假设 $D[X_1]=D[X_2]=1$，因此 $\theta$ 始终为 $\frac{\pi}{4}$。

Q2: $\rho$ 能决定什么？

A2: 两者的相关系数 $\rho$ 决定了图中椭圆的宽度。当相关越大，椭圆就显得越窄，在极限情况下变为一条直线，此时相关系数 $\rho=1$，表示完全线性相关。

多元相关